The series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
To solve the problem, we need to analyze the circuit step-by-step. We have two batteries in series and a parallel combination of two resistors.
Step 1: Understand the Circuit Configuration
We have two batteries, both with an emf (electromotive force) of 10 V:
- Battery 1: E1=10V, r1=20Ω
- Battery 2: E2=10V, r2=5Ω
These batteries are connected in series, so the total emf Etotal is:
Etotal=E1+E2=10V+10V=20V
Step 2: Calculate the Total Internal Resistance
The total internal resistance Rinternal of the batteries in series is:
Rinternal=r1+r2=20Ω+5Ω=25Ω
Step 3: Analyze the Parallel Resistor Configuration
The total voltage across the parallel combination of the resistors (30 Ω and R Ω) is equal to the voltage across the batteries. The voltage across the battery with internal resistance 20 Ω is given to be zero. This means that the entire voltage drop occurs across the internal resistance of the second battery (5 Ω).
Step 4: Set Up the Voltage Equation
Since the voltage across the battery with internal resistance 20 Ω is zero, the voltage across the 5 Ω internal resistance must equal the total voltage (20 V):
Vinternal5Ω=20V
The current I flowing through the circuit can be calculated using Ohm's law:
I=VR=20V25Ω=0.8A
Step 5: Determine the Voltage Across the Parallel Resistors
The voltage across the parallel resistors (30 Ω and R) can be calculated as:
Vparallel=I⋅r2=0.8A⋅5Ω=4V
Step 6: Set Up the Equation for the Parallel Resistors
The voltage across the parallel resistors must equal the voltage across the internal resistance of the second battery. Therefore, we have:
Vparallel30Ω+VparallelR=I
Substituting Vparallel=4V:
430+4R=0.8
Step 7: Solve for R
Rearranging the equation gives:
4R=0.8−430
Calculating 430=215:
0.8=1215
So,
4R=1215−215=1015=23
Now, cross-multiplying gives:
4⋅3=2R⟹12=2R⟹R=6Ω
Final Answer
The value of R is 6Ω.
---
We have two batteries, both with an emf (electromotive force) of 10 V:
- Battery 1: E1=10V, r1=20Ω
- Battery 2: E2=10V, r2=5Ω
Etotal=E1+E2=10V+10V=20V
The total internal resistance Rinternal of the batteries in series is:
Rinternal=r1+r2=20Ω+5Ω=25Ω
The total voltage across the parallel combination of the resistors (30 Ω and R Ω) is equal to the voltage across the batteries. The voltage across the battery with internal resistance 20 Ω is given to be zero. This means that the entire voltage drop occurs across the internal resistance of the second battery (5 Ω).
Since the voltage across the battery with internal resistance 20 Ω is zero, the voltage across the 5 Ω internal resistance must equal the total voltage (20 V):
Vinternal5Ω=20V
The current I flowing through the circuit can be calculated using Ohm's law:
I=VR=20V25Ω=0.8A
The voltage across the parallel resistors (30 Ω and R) can be calculated as:
Vparallel=I⋅r2=0.8A⋅5Ω=4V
The voltage across the parallel resistors must equal the voltage across the internal resistance of the second battery. Therefore, we have:
Vparallel30Ω+VparallelR=I
Substituting Vparallel=4V:
430+4R=0.8
Rearranging the equation gives:
4R=0.8−430
Calculating 430=215:
0.8=1215
So,
4R=1215−215=1015=23
Now, cross-multiplying gives:
4⋅3=2R⟹12=2R⟹R=6Ω
The value of R is 6Ω.
Topper's Solved these Questions
Similar Questions
The series combination of two batteries, both of the same emf 10 V, but different internal resistance of 10Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R (in Ω ) is : _________.
View SolutionThe series combination of two batteries, both of the same emf 20 V, but different internal resistance of 10Ωand2Ω,isco∩ected→theparal≤lcomb∈ationoftworesis→rs10ohmandROmega.Thevo<a≥d⇔erenceacrossthebaeryof∫ernalresistance10 Omegaiszero,thevalueofR (in Omega) is _________.
View Solution
Knowledge Check
Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
A32VB53VC35VD2VWhat is the effective resistance (in Ω ) of two resistors 20Ωand30Ω connected in parallel?
A50B12C24D25Two resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing thrpough the battery ?
A4AB43AC417AD1A
A cell of emf 2V and internal resistance 4Ω is connected across a parallel combination of two resistors of resistance 10Ω and 20Ω. Find the current through each resistor using Kirchhoff's laws.
View SolutionA battery of emf 5V and internal resistance 20Ω is connected to a combination of two resistance 50Ω and 40Ω in series. If the p.d. across the 50Ω resistor is measured by a voltmeter of resistance 1000Ω, what will be the percentage error?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionTwo sources of emf 6V and internal resistance 3Ω and 2Ω are connected to anexternal resistance R as shown. If potential difference across battery A is zero, then the value of R ( in Ω) is
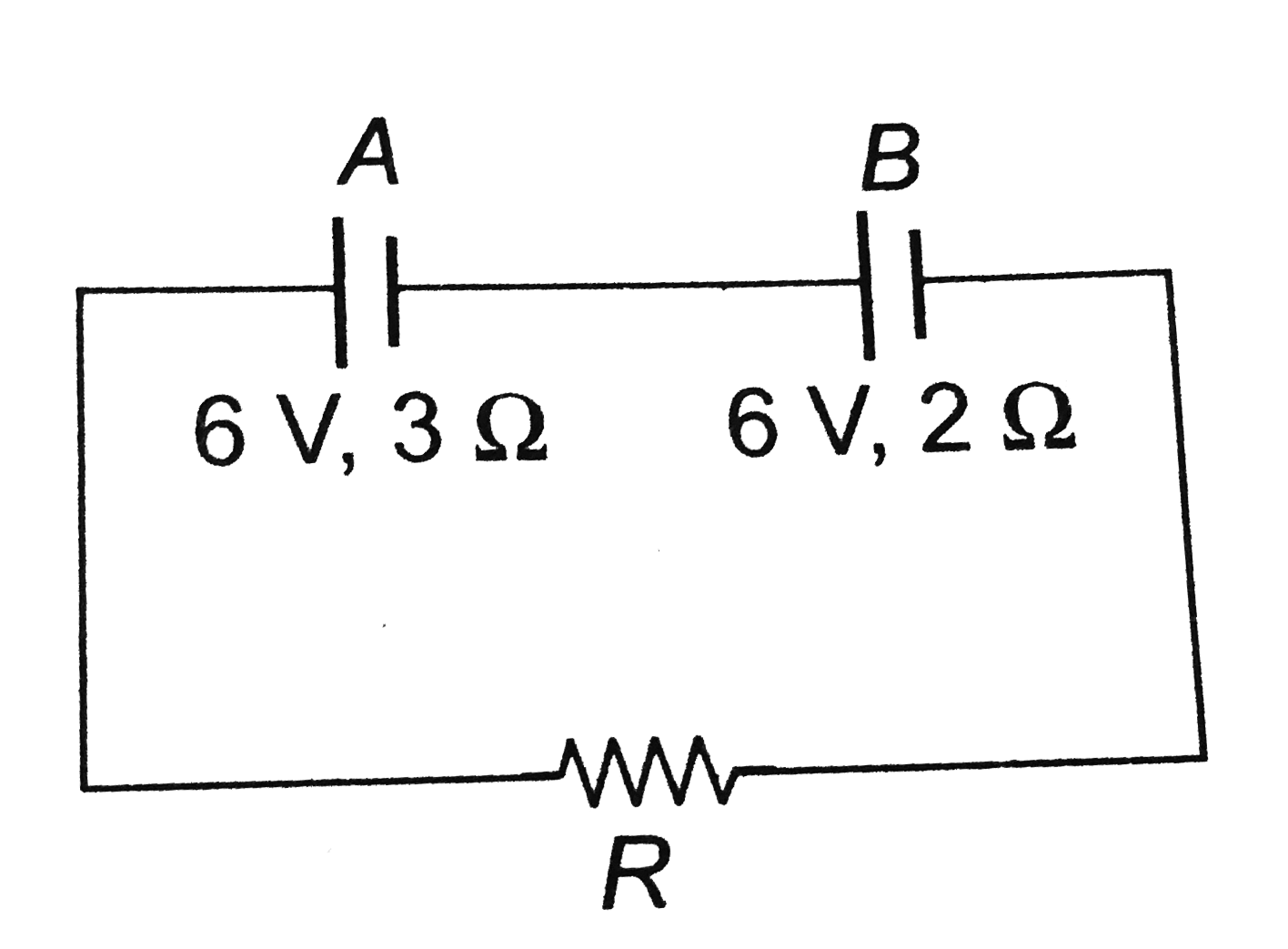
View SolutionA series combination of two resistors 1Ω each is connected to a 12 V battery of internal resistance 0.4Ω. The current flowing through it will be
View Solution
