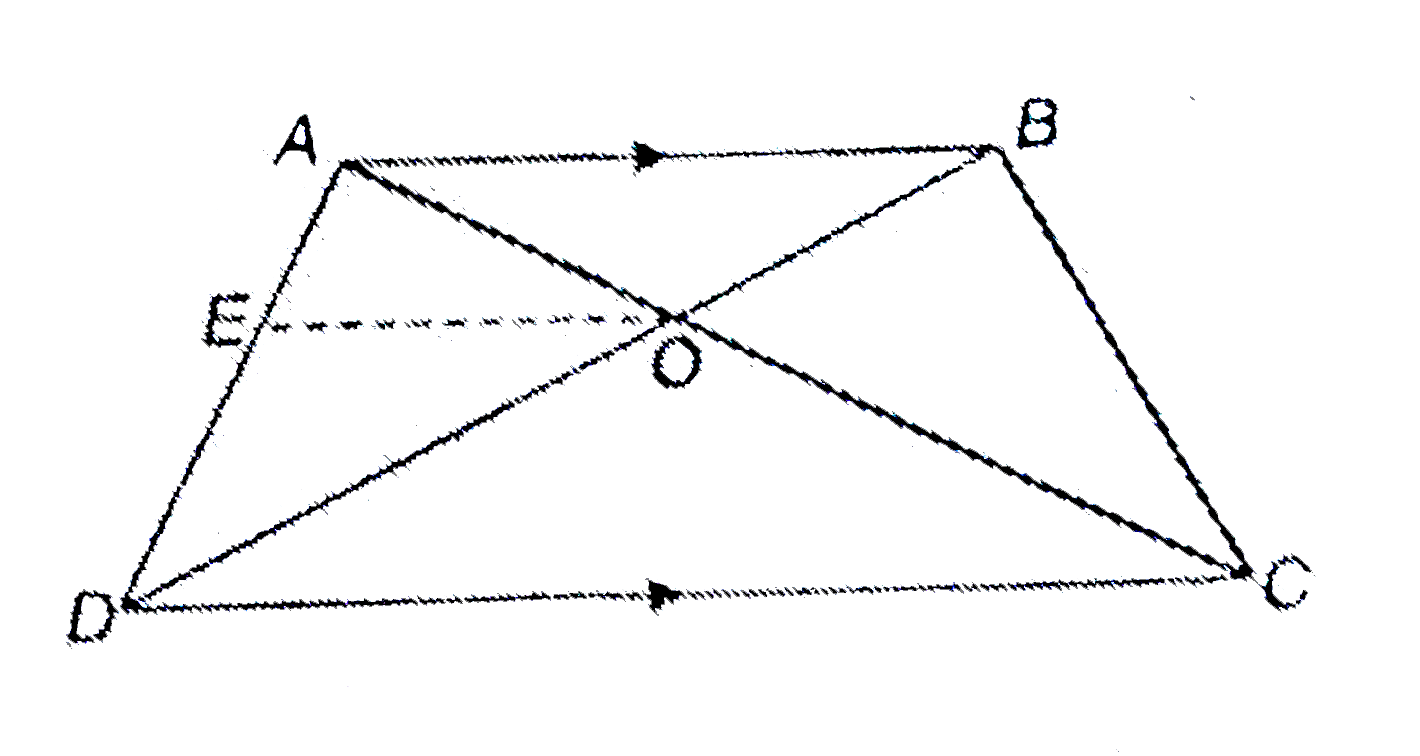
ABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
Step by step video & image solution for ABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that (A O)/(B O)=(C O)/(D O). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - HOTS (High Order Thinking Skills)
7 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (VERY SHORT ANSWER QUESTIONS)
14 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER QUESTIONS-II
24 Videos
- REAL NUMBERSBOOK - VK GLOBAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self -Assessment Test
11 Videos
- VALUE-BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-VII : (Statistics & Probability)
8 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A1:4B1:2C4:1D2:1ABCD is a trapezium in which AB∣∣CD and AB=2CD. It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A1:2B2:1C1:4D4:1ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A1:4B1:2C4:1D2:1
ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
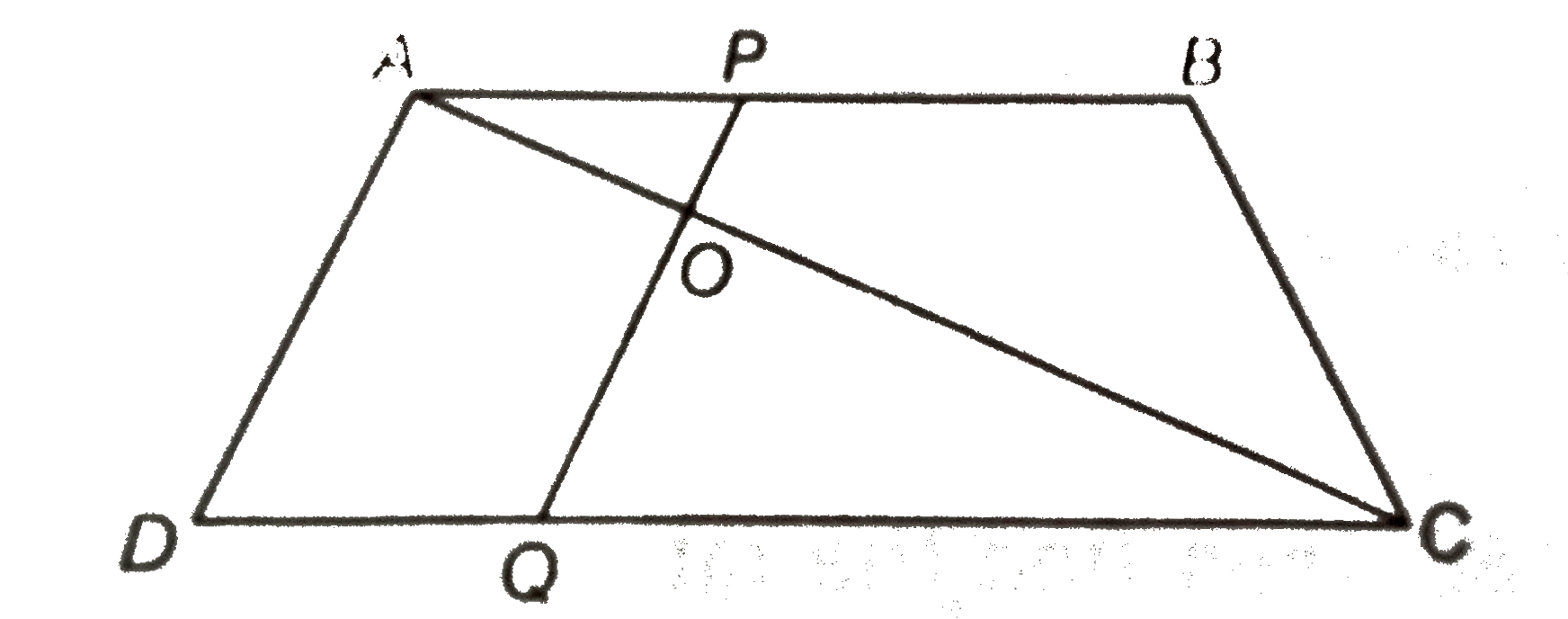
View SolutionIn figure , if AB||DC and AC, PQ intersect each other at the point O. Prove that OA.CQ=OC.AP.
View SolutionABCD is a trapezium such that BC∣∣AD and AB=4cm . If the diagonals AC and BD intersect at O such that AOOC=DOOB=12 , then BC= 7cm (b) 8cm (c) 9cm (d) 6cm
View SolutionABCD is a trapezium in which ABCD . The diagonals AC and BD intersect at O . Prove that (i) AOBCOD (ii) If OA=6cm , OC=8cm , Find: Area (AOB)Area (COD) (b) Area (AOD)Area (COD)
View SolutionABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
View Solution
