O is the a point in the interior of ΔABC,OD⊥BC,OE⊥ACandACandOF⊥AB, as shown in the figure,
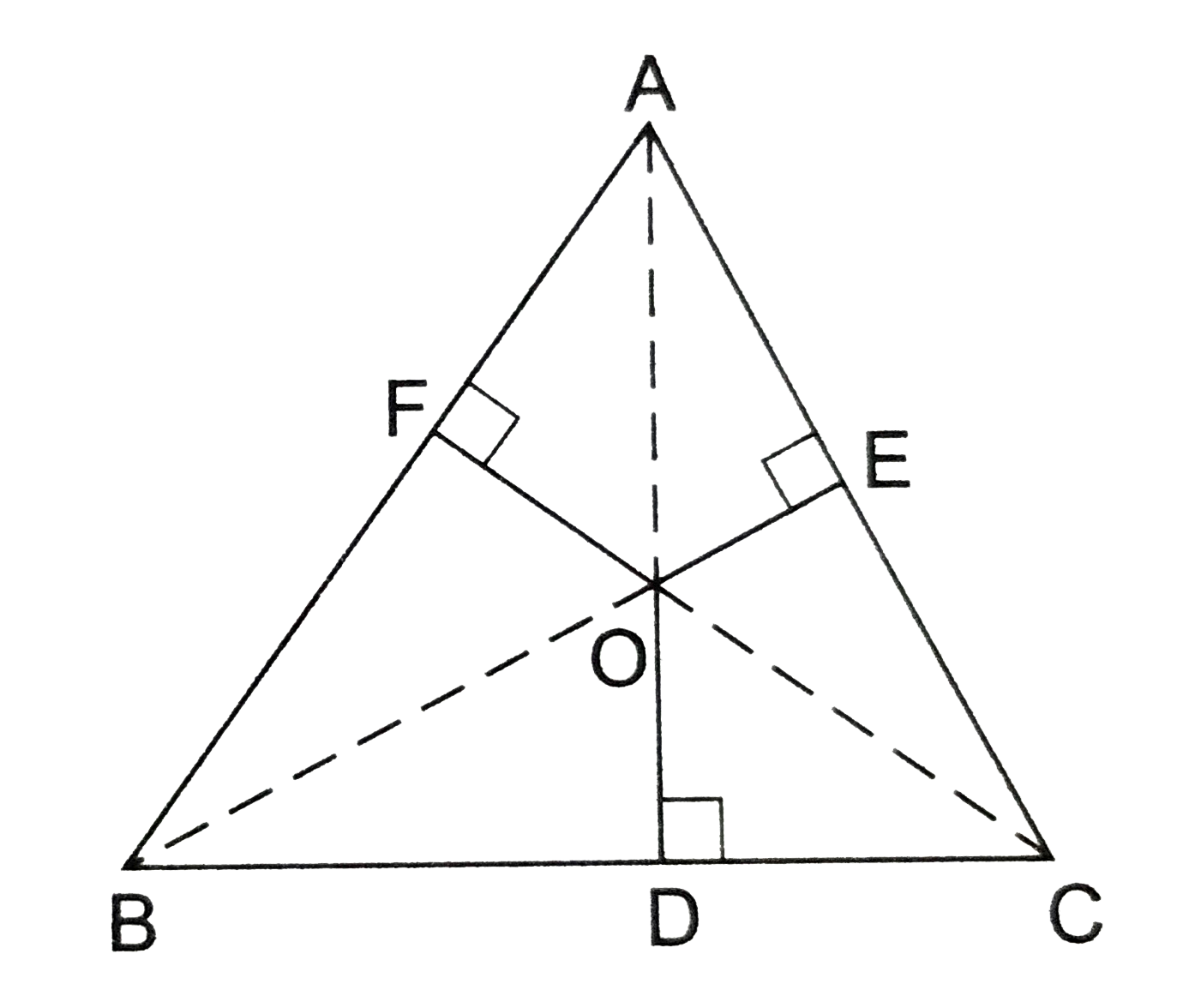
Prove that :
(i)OA2+OB2+OC2−OD2−OD2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD2
Step by step video & image solution for O is the a point in the interior of Delta ABC, OD bot BC, OE bot AC and AC and OF bot AB, as shown in the figure, Prove that : (i) OA^(2)+OB^(2)+OC^(2)-OD^(2)-OD^(2)-OF^(2)=AF^(2)+BD^(2)+CE^(2) (ii) AF^(2)+BD^(2)+CE^(2)=AD^(2)+BF^(2)+CD^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - HOTS (High Order Thinking Skills)
7 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (VERY SHORT ANSWER QUESTIONS)
14 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER QUESTIONS-II
24 Videos
- REAL NUMBERSBOOK - VK GLOBAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self -Assessment Test
11 Videos
- VALUE-BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-VII : (Statistics & Probability)
8 Videos
Similar Questions
O is a point in the interior of ΔABC,OD⊥BC,OE⊥ACandOF⊥AB, as shown in the figure,

Prove that :
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD2
View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionIn the figure given below O is a point in the interior of a triangle ABC , OD ⊥ BC ,OE ⊥ AC and OF⊥AB . Show that
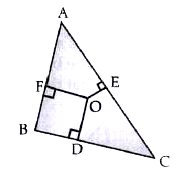
AF2+BD2+CE2=AE2+CD2+BF2
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
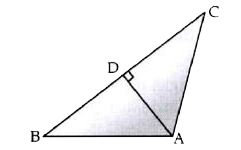
View SolutionABCD is a rhombus. Prove that AB2+BC2+CD2+DA2=AC2+BD2
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
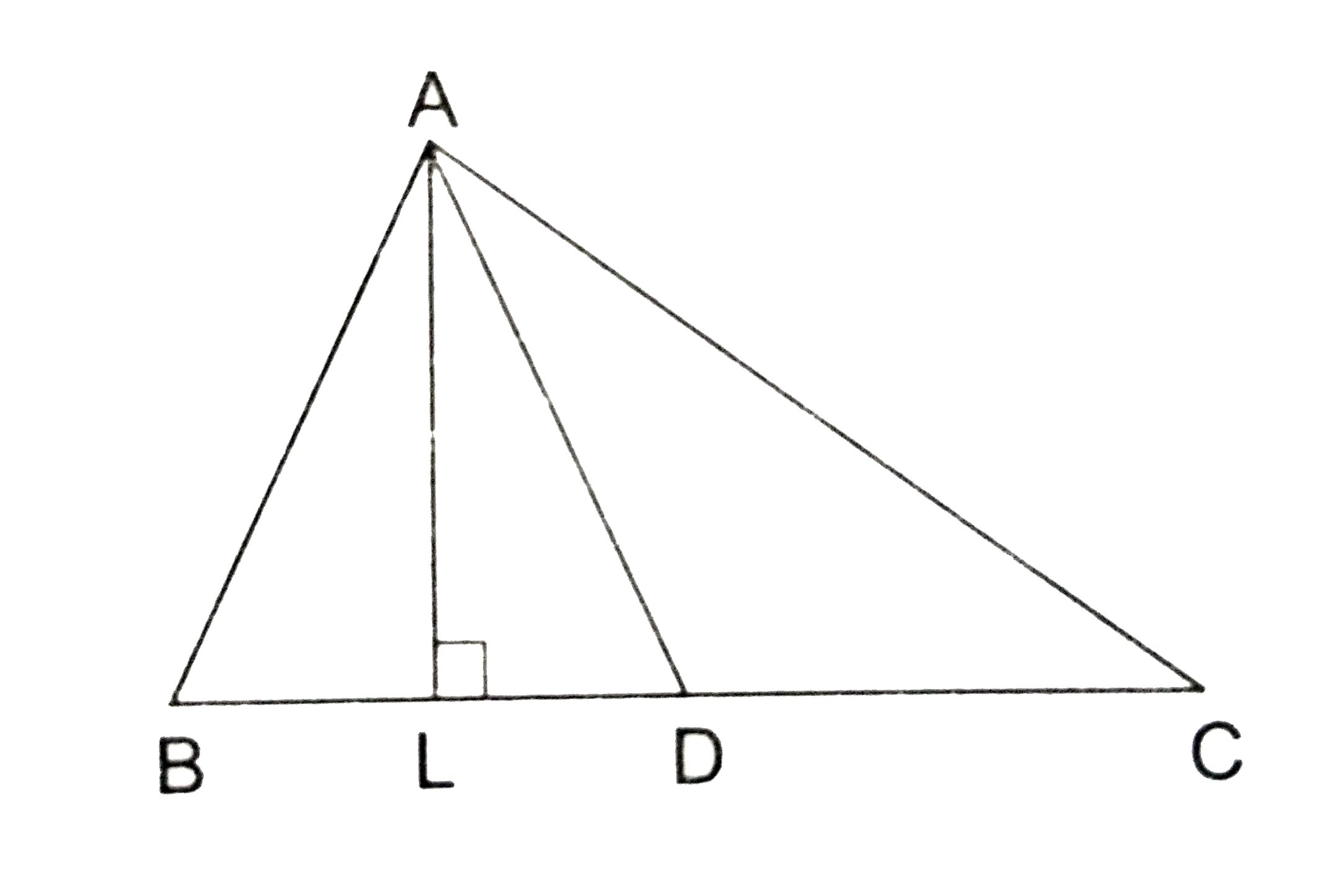
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View Solution
