In Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
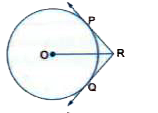
Step by step video & image solution for In Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If anglePRQ = 120 ^@ , then prove that OR = PR + RQ . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Long Answer Questions 4 mark)
12 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
Similar Questions
Knowledge Check
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
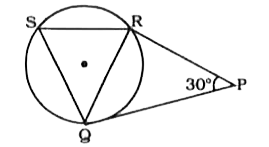 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘In the figure , if TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘, then ∠OPQ =
 A25∘B60∘C40∘D30∘
A25∘B60∘C40∘D30∘
In the figure-3, from an external point P, two tangents PQ and PR are drawn to a circle of the radius 4 cm with centre O. If ∠ QPR = 90∘, then length of PQ is
View SolutionTheorem: The length of two tangents drawn from an external point to a circle are equal.
View SolutionThe lengths of tangents drawn from an external point to a circle are ________.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View SolutionTwo tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of 100∘ then what is the value of ∠BOC.
View SolutionIf from an external point P of a circle with centre O, two tangents PQ and PR are drawn such ∠QPR=120∘, prove that 2PQ=PO.
View Solution
