In figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABDΔECF.
Step by step video & image solution for In figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If A D_|_B CandE F_|_A C, prove thatDeltaA B D DeltaE C F. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MODEL QUESTION PAPER - 9 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 9 [UNSOLVED]EXERCISE - SECTION - D
7 Videos
- MODEL QUESTION PAPER - 9 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 9 [UNSOLVED]EXERCISE - SECTION - B
6 Videos
- MODEL QUESTION PAPER - 1 BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 1 EXERCISE - SECTION - C
15 Videos
- MODEL QUESTION PAPER -2 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -2 [UNSOLVED]EXERCISE - SECTION-D
10 Videos
Similar Questions
In Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn the given figure, E is a point on side CB produced of an isosceles ΔABC with AB=AC.. If AD⊥BCandEF⊥AC, prove tha ΔABD~ΔECF
View Solution
Knowledge Check
D,E and F are the middle points of the sides of the triangle ABC, then
Acentroid of the triangle DEF is the same as that of ABCBorthocentre of the traiangl DRF is the circumcentre of ABCCorthocentre of the triangle DEF is the incentre of ABCDcentroid of the triangle DEF is not the same as that of ABC
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

View SolutionDandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
View SolutionThe incircle of an isosceles triangle ABC, with AB=AC, touches the sides AB, BC, CA at D,E and F respectively. Prove that E bisects BC.
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
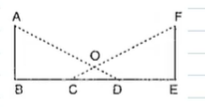
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2

View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
View Solution
