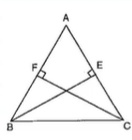
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
In △ABC,
we have
ABAC
∠B=∠C........(i)
In △ADE,
AD=AE
∠D=∠E..........(ii)
We can write
∠A+∠D+∠E=∠A+∠B+∠C
2∠D=2∠C
or
∠D=∠C.......(iii)
Now
∠ADE+∠BDE=180∘But
∠ADE=∠BCE
[Using (i)and(ii)(iii)[Linear pair]{By (iii)]
∠BCE+∠BDE=180∘
⇒B,C,EandD are concyclic.
Topper's Solved these Questions
Similar Questions
DandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
View SolutionD and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
 View Solution
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
 View Solution
View Solution

