Consider Example 6.8 taking the coefficient of friction, u, to be 0.5 and calculate the maximum compression of the spring.
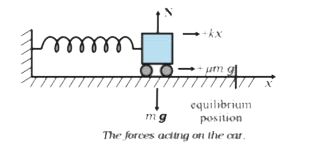
In presence of friction, both the spring force and the frictional force act so as to oppose the compression of the spring as shown in Fig. 6.9.
We invoke the work-energy theorem, rather than the conservation of mechanical energy.
The change in kinetic energy is
△K=Kf−Kt=0−12mv2
The work done by the net force is
W=−12kx2m−μmgxm
Equatting we have
12mv2=12kx2m+μmgxm
Now μmg=0.5×103×10=5×103N (taking g=10.0ms−2). After rearranging the above equation we obtain the following quadratic equation in the unknown xm.
kx2m+2μmgxm−mv2=O
xm=−μmg+[μ2m2g2+mkv2]12k
where we take the positive square root since xm is positive. Putting in numerical values we obtain xm=1.35m
which, as expected, is less than the result in Example 6.8.
If the two forces on the body consist of a conservative force Fc and a non-conservative force Fnc, the conservation of mechanical energy formula will have to be modified. By the WE theorem
(Fc+Fnc)△x=△K
But Fc△x=−△V
Hence, △(K+V)=Fnc△x
△E=Fnc△x
where E is the total mechanical energy. Over the path this assumes the form
Ef−Et=Wnc
where Wnc is the total work done by the non-conservative forces over the path. Note that unlike the conservative force, Wnc depends on the particular path i to f.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - NCERT BANGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES
44 Videos
- WORK, ENERGY AND POWERBOOK - NCERT BANGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES (ADDITIONAL EXERCISES)
6 Videos
- WAVESBOOK - NCERT BANGLISHCHAPTER - WAVESEXERCISE - Exercises
26 Videos
Similar Questions
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
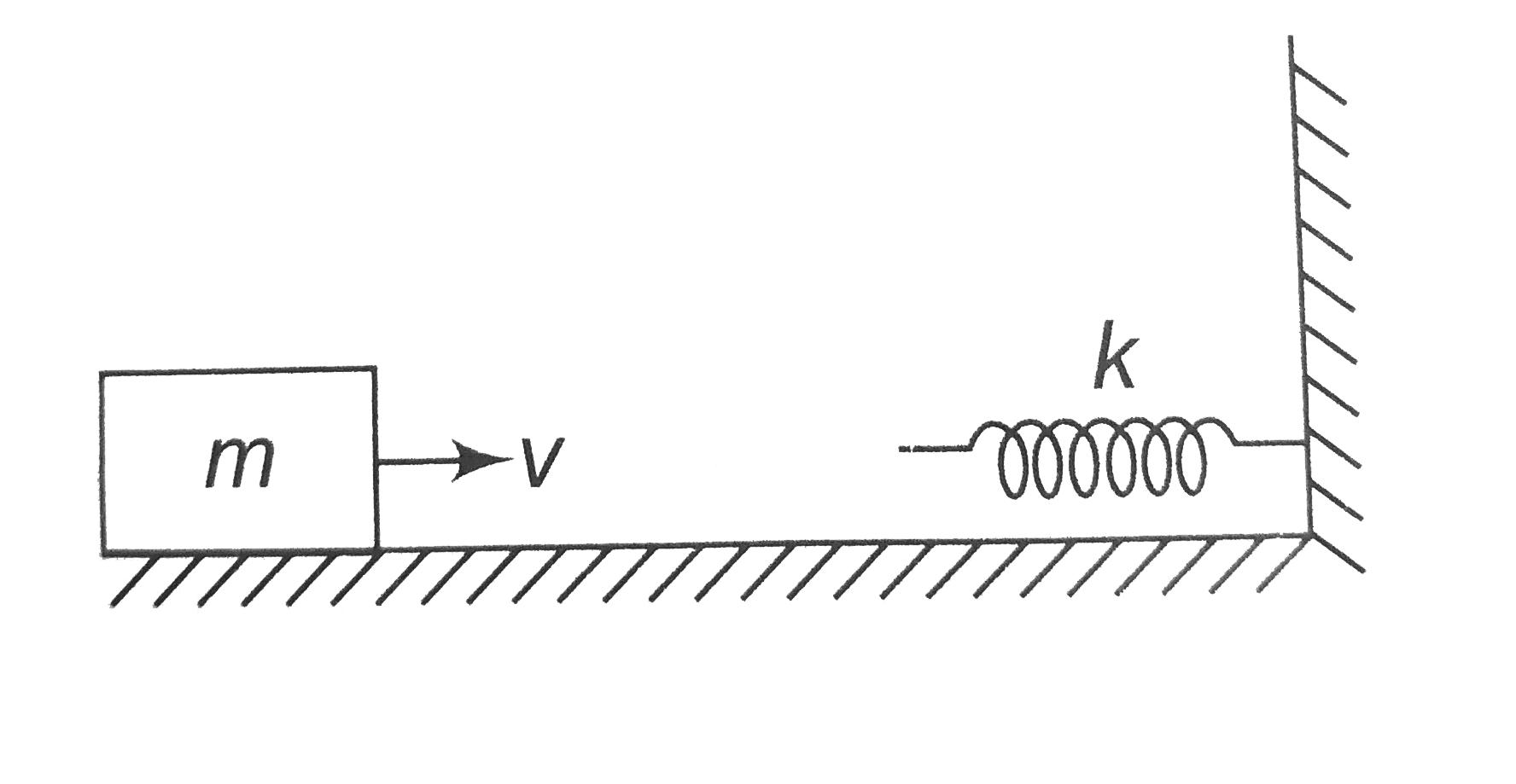 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
Asin−1(0.2)Bcos−1(0.2)Ctan−1(0.1)Dcot−1(5)
Consider example 25, taking the coefficient of friction μ to be 0.4 and calculate the maximum compression of the spring (g=10ms−2)
View SolutionConsider Example 22. Takin the coefficient of friction, μ to be 0.5, calculate the maximum compression of the spring.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View Solution .
.
In the figure shown, AB=BC=2m. Friction coefficient everywhere is μ=0.2. Find the maximum compression of the spring.
View Solution
