Let O(0, 0) and (0, 1) be two fixed points, then the locus of a point P such that the perimeter of $Δ A O P$ is 4, is

A

$8 x^{2} - 9 y^{2} + 9 y = 18$

B

$9 x^{2} - 8 y^{2} + 8 y = 16$

C

$9 x^{2} + 8 y^{2} - 8 y = 16$

D

$8 x^{2} + 9 y^{2} - 9 y = 18$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given vertices of $Δ A O P$ are O(0, 0) and A(0, 1)
Let the coordinates of point P are (x, y)
Clearly, perimeter = OA + AP + OP = 4 (given)
$\Rightarrow \sqrt{{(0 - 0)}^{2} + {(0 - 1)}^{2}} + \sqrt{{(0 - x)}^{2} + {(1 - y)}^{2}} + \sqrt{x^{2} + y^{2}} = 4$
$\Rightarrow 1 + \sqrt{x^{2} + {(y - 1)}^{2}} + \sqrt{x^{2} + y^{2}} = 4$
$\Rightarrow \sqrt{x^{2} + y^{2} - 2 y + 1} + \sqrt{x^{2} + y^{2}} = 3$
$\Rightarrow x^{2} + y^{2} - 2 y + 1 = 3 - \sqrt{x^{2} + y^{2}}$
$\Rightarrow x^{2} + y^{2} - 2 y + 1 = 9 + x^{2} + y^{2} - 6 \sqrt{x^{2} + y^{2}}$
[squaring both sides ]
$\Rightarrow 1 - 2 y = 9 - 6 \sqrt{x^{2} + y^{2}}$
$\Rightarrow 6 \sqrt{x^{2} + y^{2}} = 2 y + 8$
$\Rightarrow 3 \sqrt{x^{2} + y^{2}} = y + 4$
$\Rightarrow 9 (x^{2} + y^{2}) = {(y + 4)}^{2}$ [ squaring both sides]
$\Rightarrow 9 x^{2} + 9 y^{2} = y^{2} + 8 y + 16$
$\Rightarrow 9 x^{2} + 8 y^{2} - 8 y = 16$
Thus, the locus of point P(x,y) is
$9 x^{2} + 8 y^{2} - 8 y = 16$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $A = (4, 0), B = (0, 12)$ be two points in the plane. The locus of a point C such that the area of triangle ABC is 18 sq. units is -
A ${(y + 3 x + 12)}^{2} = 81$
B ${(y + 3 x + 81)}^{2} = 12$
C ${(y + 3 x - 12)}^{2} = 81$
D ${(y + 3 x - 81)}^{2} = 12$
Question 2 - Select One
A and B are two fixed points. The locus of a point P such that $∠ A P B$ is a right angle, is:

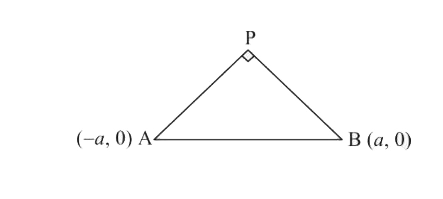A $x^{2} + y^{2} = a^{2}$
B $x^{2} - y^{2} = a^{2}$
C $2 x^{2} + y^{2} = a^{2}$
DNone of these

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 5 Integer Answer type Question

Home
Ask Doubt
Profile