Let ABCD be a square of side length 2 units. C2 is the circle through vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. 27. If P is a point on C1 and Q in another point on C2, then 2222 2222 PA PB PC PD QA QB QC QD +++ +++ is equal to (A) 0.75 (B) 1.25 (C) 1 (D) 0.5

A

0.75

B

1.25

C

1

D

0.5

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Let the, equation of circle are
C1:(x−1)2+(y−1)2=(1)2
andC2:(x−1)2+(y−1)2=(√2)2
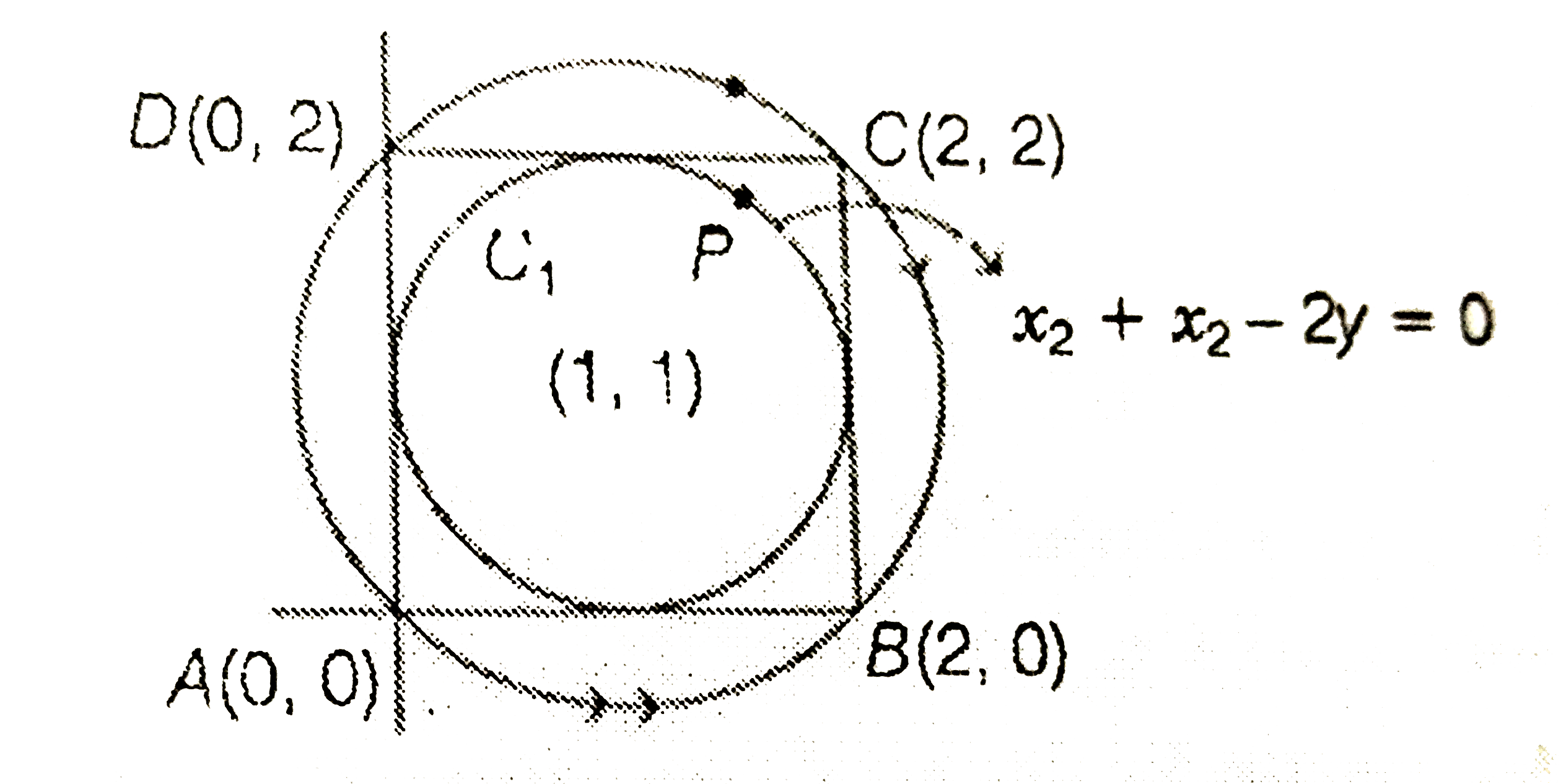
ocr_image
∴c∞rd∈atesofP(1+cosθ,1+sinθ)
and Q(1+√2cosθ,0,1+√2sinθ)
PA2+PB2+PC2+PD2
={(1+cosθ)2+(1+sinθ)2}+{(cosθ−1)2+(1+sinθ)2}
+{(cosθ−1)2+(sinθ−1)2}
+{(1+cosθ)2+(sinθ−1)2}=12
Similarly, QA2+QB2+QC2+QD2=16
∴∑PA2∑QA2=1216=0.75

Updated on:21/07/2023
|
Class 12MATHSCIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let ABCD be a square of side length 2 units. C2 is the fircle through the vertices A, B, C, D and C1 is the circle touching all the of the square ABCD. L is a lien through vertex A. A circle touches the line L and the circle C1 externally such that both the circles are on the same side of the line L. The locus of the centre of the circle is

    Aellipse
    Bhyperbola
    Cparabola
    Dpair of straight lines

  • Let ABCD be a square of side length 2 units. C2 is the fircle through the vertices A, B, C, D and C1 is the circle touching all the of the square ABCD. L is a lien through vertex A. A circle touches the line L and the circle C1 externally such that both the circles are on the same side of the line L. The locus of the centre of the circle is

    Aan ellipse
    Ba hyperbola
    Ca parabola
    Da pair of straight lines

  • Let ABCD be square of side length 2 unit. C2 is the circle through verticles A,B,C,D and C1 is the circle touching all the sides of square ABCD. L is the line through A. A circle touches the line L and the circle C1 exrternally such that both the circles are on the same side of the line, then the locus of centre of the circle is

    Aellipse
    Bhyperbola
    Cparabola
    Dparts of straight line