Let $A B C D$ be a quadrilateral with are $18$ , side $A B$ parallel to the side $C D, a n d A B = 2 C D$ . Let $A D$ be perpendicular to $A B a n d C D$ . If a circle is drawn inside the quadrilateral $A B C D$ touching all the sides, then its radius is $3$ (b) 2 (c) $\frac{3}{2}$ (d) 1

A

3

B

2

C

$\frac{3}{2}$

D

1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$18 = \frac{1}{2} (3 a) (2 r)$
$\Rightarrow ar = 6$
Line $y = - \frac{2 r}{α} (x - 2 α)$ is tangent to circle
${(x - r)}^{2} + {(y - r)}^{2} = r^{2}$
$2 α = 3 r, a r = 6 and r = 2$

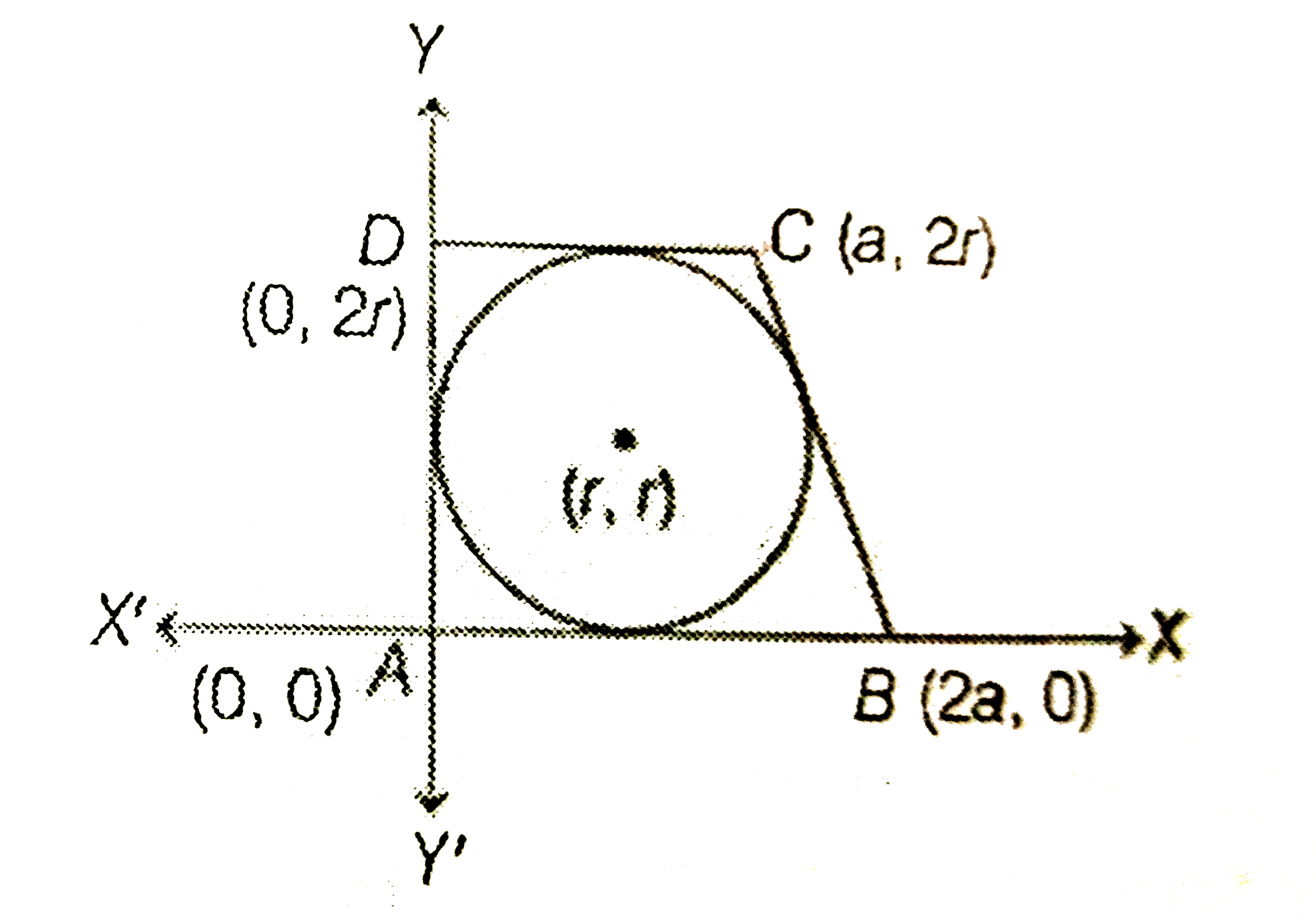
Alternative Solution
$\frac{1}{2} (x + 2 x) \times 2 r = 18$
$x r = 6 ... (i)$
In $Δ A O B, tan θ = \frac{x - r}{r}$
and "in" $Δ D O C$ ,
$tan (90^{\circ} - θ) = \frac{2 x - r}{r}$
$∴ \frac{x - r}{r} = \frac{r}{2 x - r}$
$\Rightarrow x (2 x - 3 x) = 0$
$\Rightarrow x = \frac{3 r}{2} ... (i i)$
From Eqs. (i) and (ii), we get
r = 2

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 3 Equation of Tangent, Normal and Length of Tangents

Home
Ask Doubt
Profile