Let $S \equiv x^{2} + y^{2} + 2 g x + 2 f y + c =$ be a given circle. Find the locus of the foot of the perpendicular drawn from the origin upon any chord of S which subtends a right angle at the origin.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $x^{2} + y^{2} + g x + f y + \frac{c}{2} = 0$

Let P (h,k) be the foot of perpendicular drawn from origin O(0, 0) on the chord AB of the given circle such that the chord AB subtenda a right angle at the origin.

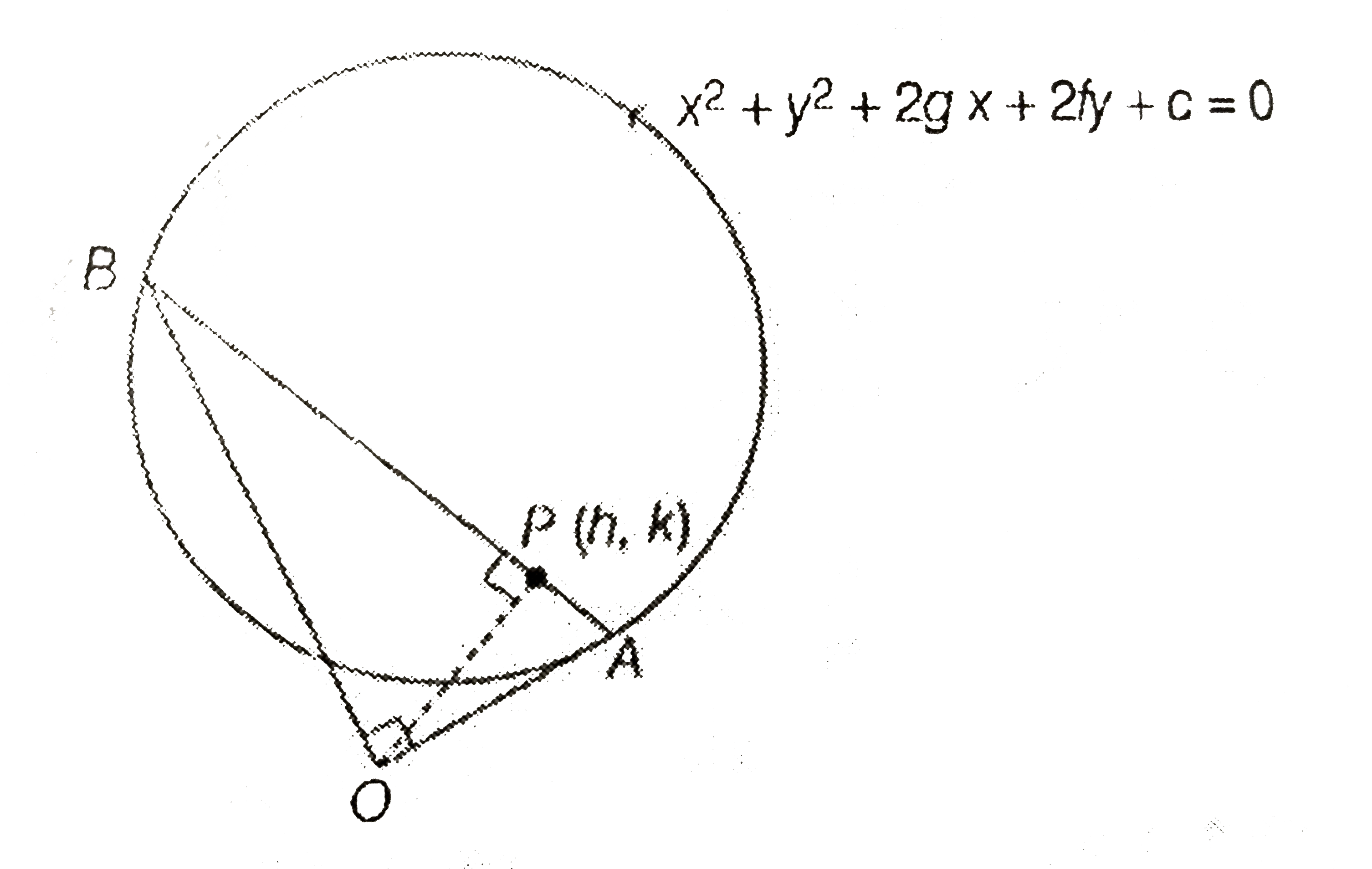
The equation of chord AB is
$y - k = - \frac{h}{k} (x - h) \Rightarrow h x + k y = h^{2} + k^{2}$
The combined equaition of OA and OB is homogenous equation of second degree obtained by the help of the given circle and the chord AB and is given by,
$x^{2} + y^{2} + (2 g x + 2 f y) (\frac{h x + k y}{h^{2} + k^{2}}) + c {(\frac{h x + k y}{h^{2} + k^{2}})}^{2} = 0$
Since, the lines OA and OB are at right angle.
$∴$ Coefficient of $x^{2}$ + coefficient of $y^{2}$ = 0
$\Rightarrow {1 + \frac{2 g h}{h^{2} + k^{2}} + \frac{c h^{2}}{{(h^{2} + k^{2})}^{2}}}$
$+ {1 + \frac{2 f k}{h^{2} + k^{2}} + \frac{c k^{2}}{{(h^{2} + k^{2})}^{2}}} = 0$
$\Rightarrow 2 (h^{2} + k^{2}) + 2 (g h + f k) + c = 0$
$\Rightarrow h^{2} + k^{2} + g h + f k + \frac{c}{2} = 0$
$∴$ Required equation of locus is
$x^{2} + y^{2} + g x + f y + \frac{c}{2} = 0$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The foot of the perpendicular drawn from the origin to the plane $x + y + z = 3$ is
A $(0, 1, 2)$
B $(0, 0, 3)$
C $(1, 1, 1)$
D $(- 1, 1, 3)$
The coordinates of the foot of perpendicular drawn from the origin to the plane 2x+y-2z=18 are ……
A(4,2,4)
B(-4,2,4)
C(-4,-2,4)
D(4,2,-4)
Foot of perpendicular drawn from the origin to the plane $2 x - 3 y + 4 z = 29$ is
A $(7, - 1, 3)$
B $(5 - 1, 4)$
C $(5, - 2, 3)$
D $(2, - 3, 4)$

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 4 Analytical & Descriptive Questions

Home
Ask Doubt
Profile