Let a given line $L_{1}$ intersect the X and Y axes at P and Q respectively. Let another line $L_{2}$ perpendicular to $L_{1}$ cut the X and Y-axes at Rand S, respectively. Show that the locus of the point of intersection of the line PS and QR is a circle passing through the origin

Video Solution

Text Solution

Verified by Experts

Let the equation of $L_{)} 1)$ be $x cos α + y sin α = P_{1}$
Then, any line perpendicular to $L_{1}$ is

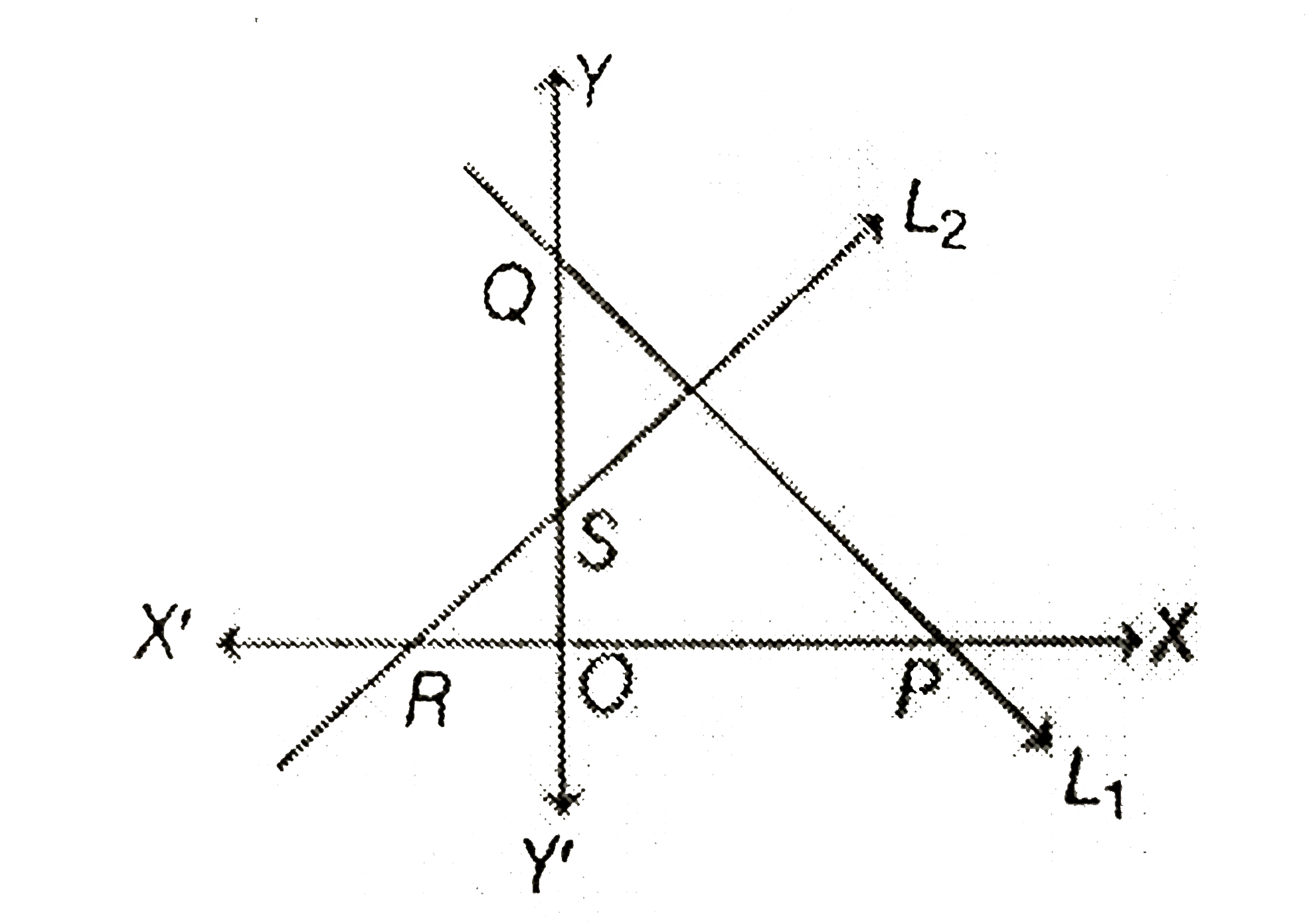
$x sin α - y cos α = p_{2}$
where, $p_{2}$ is a variable.
Then, $L_{1}$ meets X-axis at P $(p_{1} sec α, 0)$ and Y-axis at $Q (0, p_{1} cos e c α)$ .
Similarly, $L_{1}$ meets X-axis at $R (p_{2} cos e c α, 0)$ and Y-axis at S $(0, - p_{2} sec α)$ .
Now, equation of PS is,
$\frac{x}{p_{1} sec α} + \frac{y}{- p_{2} sec α} = 1 \Rightarrow \frac{x}{p_{1}} - \frac{y}{p_{2}} = sec α ... (i)$
Similarly, equation of QR is
$\frac{x}{p_{2} cos e c α} + \frac{y}{p_{1} cos e c α} = 1 \Rightarrow \frac{x}{p_{2}} - \frac{y}{p_{1}} = cos e c α ... (i i)$
Locus of point of intersection of PS and QR can be obtained by eliminating the variable $p_{2}$ from Eqs, (i) and (ii).
$∴ (\frac{x}{p_{1}} - sec α) \frac{x}{y} + \frac{y}{p_{1}} = cos e c α$
$\Rightarrow (x - p_{1} sec α) x + y^{2} = p_{1} y cosec α$
$\Rightarrow x^{2} + y^{2} - p_{1} x sec α - p_{1} y cosec α = 0$
which is a circle through origin.

Updated on:21/07/2023

A line $L_{1} = \frac{x}{10} + \frac{y}{8} = 1$ intersects the coordinate axes at points A and B. Another line $L_{2}$ perpendicular to $L_{1}$ intersects the coordinate axes at C and D. The locus of circumcentre of $Δ A B D$ is
A $5 x - 4 y = 9$
B $5 x - 4 y = 18$
C $4 x - 5 y = 9$
D $4 x - 5 y = 18$