From the origin, chords are drawn to the circle (x−1)2+y2=1. The equation of the locus of the mid-points of these chords is circle with radius
For the equation of circle x2+y2−2x=0. Let the mid-point of chords be (h,k).
∴ Equation of chord bisected at the point is S1=T.
∴h2+k2−2h=xh+yk−(x+h) which passes through (0,0).
⇒h2+k2−2h=−h
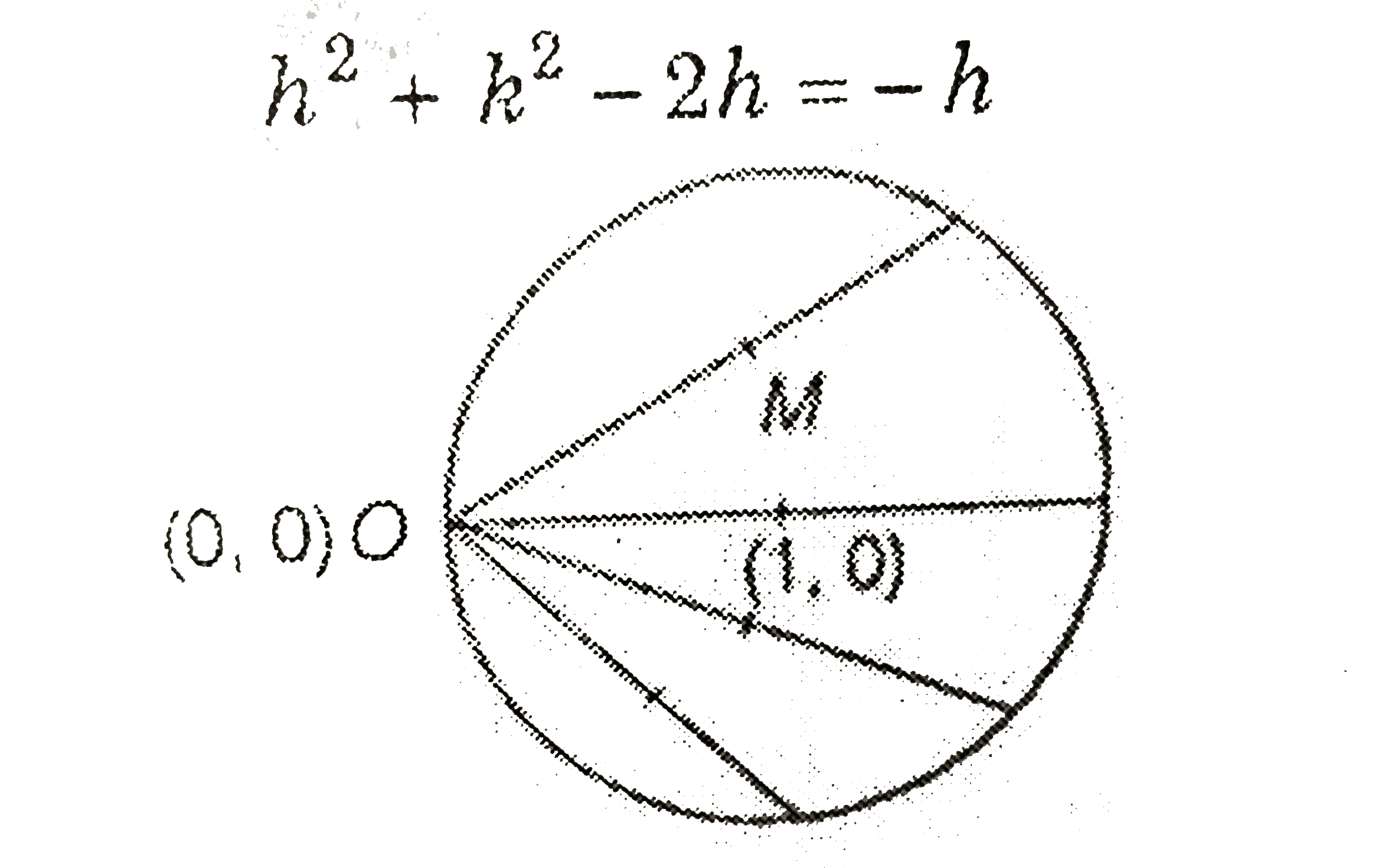 lt brgt ∴ The required locus of a chord is x2+y2−x=0
lt brgt ∴ The required locus of a chord is x2+y2−x=0
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Analytical & Descriptive Questions8videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Integer Answer type Question1videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Assertion and Reason1videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )8videos
BINOMIAL THEOREM
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)1videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
If from the origin a chord is drawn to the circle x2+y2−2x=0, then the locus of the mid point of the chord has equation
Ax2+y2+x+y=0Bx2+y2+2x+y=0Cx2+y2−x=0Dx2+y2−2x+y=0 - Question 2 - Select One
From points on the circle x2+y2=a2 tangents are drawn to the hyperbola x2−y2=a2. Then, the locus of mid-points of the chord of contact of tangents is:
A(x2−y2)2=a2(x2+y2)B(x2−y2)=a2(x2+y2)C(x2−y2)=a2(x2+y2)2DNone of these
Find the locus of the mid-points of chords of constant length in a circle
View SolutionTangents are drawn to a unit circle with centre at the origin from each point on the line 2x+y=4. Then the equation to the locus of the middle point of the chord of contact is
View SolutionThe equation of chord with mid-point P(x1,y1) to the circle S=0 is
View SolutionIf from a variable point P(−2+2cosθ,3+2sinθ), θ∈R tangents are drawn to the circle S:x2+y2+4x−6y+11=0, then as θ varies locus of mid point of corresponding chords of contact will be (1) Line x=3 (2) Circle concentric with circle S of radius 1 unit (3) Line y=3 (4) Circle concentric with circle S of radius 2units.
View SolutionFrom points on the straight line 3x-4y + 12 = 0, tangents are drawn to the circle x2+y2=4. Then, the chords of contact pass through a fixed point. The slope of the chord of the circle having this fixed point as its mid-point is
View SolutionTangents are drawn from points on the line x+2y=8 to the circle x2+y2=16. If locus of mid-point of chord of contacts of the tangents is a circles S, then radius of circle S will be
View Solution

