The tangent PT and the normal PN to the parabola y2=4ax at a point P on it meet its axis at points T and N, respectively. The locus of the centroid of the triangle PTN is a parabola whose:
vertex is (2a3,0)
directrix is x = 0
latusrectum is 2a3
focus is (a,0)
The correct Answer is:A, D
Equation of tangent and normal at point P(at2,2at) is
ty=x=at2 and y=−tx+2at+at2
Let controid of ΔPTN is R(h,k)
∴H=at2+(−at2)+2a+at23
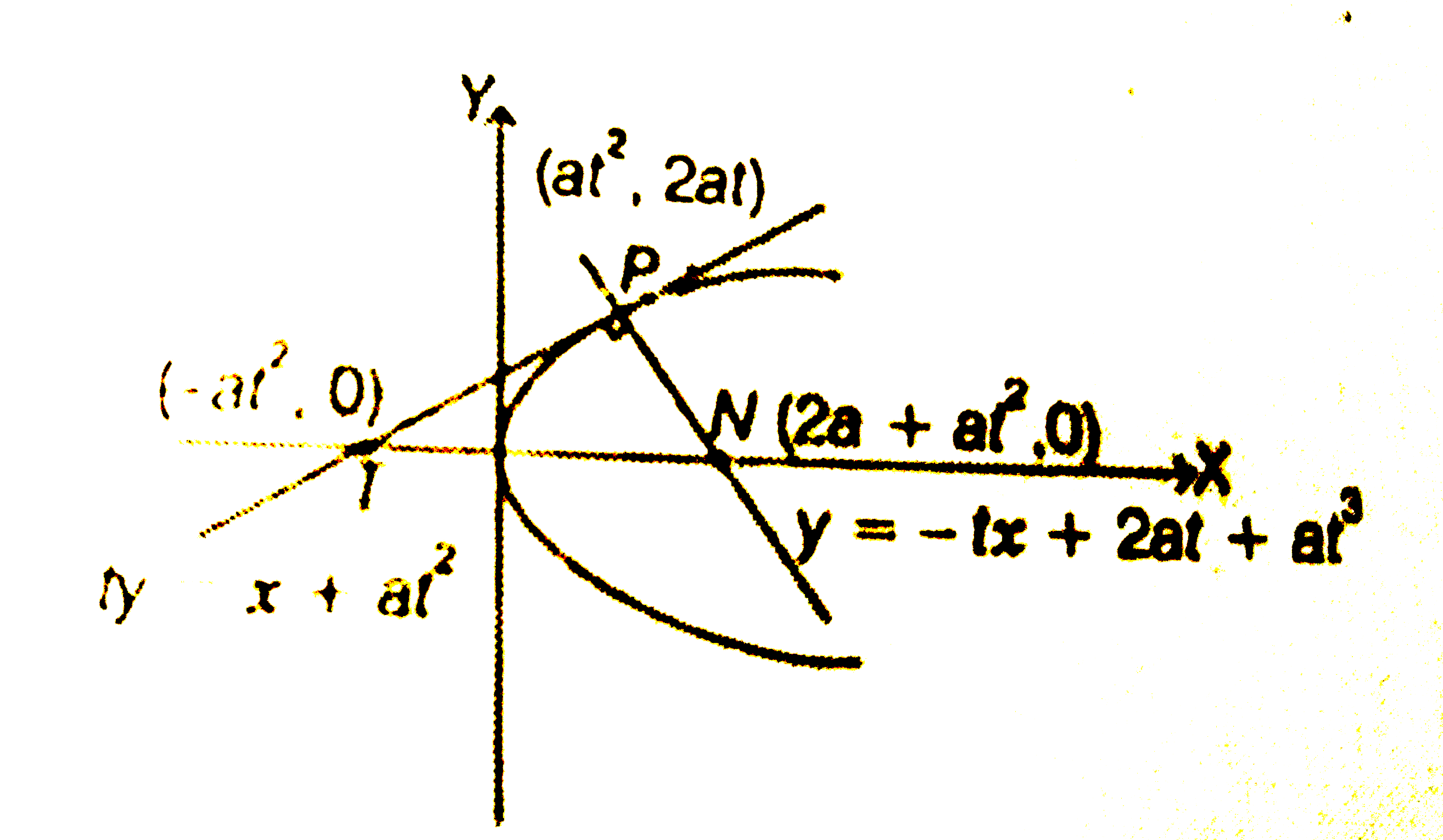
and k=2at3
⇒3h=2a+a(3k2a)2
⇒3h=2a+9k24a
⇒9k2=4a(3h−2a)
∴ Locus of centroid is
y2=4a3(x−2a3)
∴ vertex (2a3,0), directrix
x−2a3=−a3
⇒x=a3
and latusrectum =4a3
∴ Focus (a3+2a3,0) i.e., (a,0)
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (INTEGER )1videos
PARABOLA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ANALYTICAL & DESCRIPTIVE )4videos
PARABOLA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS I (MATCH THE COLUMNS )1videos
PARABOLA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS87videos
MISCELLANEOUS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Dearrangement and Number of Divisors (Fill in the Blank )1videos
PERMUTATIONS AND COMBINATIONS
Similar Questions
TP and TQ are tangents to parabola y2=4x and normals at P and Q intersect at a point R on the curve. The locus of the centre of the circle circumseribing ΔTPQ is a parabola whose
View SolutionThe tangent and normal at P(t), for all real positive t, to the parabola y2=4ax meet the axis of the parabola in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle passing through the points P,Tand G is
View Solution
Knowledge Check
- Question 1 - Select One or More
The tangent PT and the normal PN to the parabola y2=4ax at a point P on it meet its axis at points T and N, respectively. The locus of the centroid of the triangle PTN is a parabola whose:
Avertex is (2a3,0)Bdirectrix is x = 0Clatus rectum is 2a3Dfocus is (a,0) - Question 2 - Select One
The tangent and normal at the point P(4,4) to the parabola, y2=4x intersect the x-axis at the points Q and R, respectively. Then the circumcentre of the ΔPQR is
A(2,0)B(2,1)C(1,0)D(1,2) - Question 3 - Select One
The normal to the parabola y2=8ax at the point (2, 4) meets the parabola again at the point
A(-18, -12)B(-28, 12)C(18, 12)D(18, -12)
From a variable point R on the line y = 2x + 3 tangents are drawn to the parabola y2=4ax touch it at P and Q point. Find the locus of the centroid of the triangle PQR.
View SolutionThe normal meet the parabola y2=4ax at that point where the abscissa of the point is equal to the ordinate of the point is
View SolutionThe tangent and normal at the point P[at2,2at) to the parabola y2=4ax meet the x-axis in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle through T, P, G is
View SolutionThe normal meet the parabola y2=4ax at that point where the abscissa of the point is equal to the ordinate of the point is
View SolutionTangent and normal at any point P of the parabola y2=4ax(a>0) meet the x-axis at T and N respectively. If the lengths of sub-tangent and sub-normal at this point are equal, then the area of ΔPTN is given by
View Solution

