Show that the locus of a point that divides a chord of slope $2$ of the parabola $y^{2} = 4 x$ internally in the ratio $1 : 2$ is parabola. Find the vertex of this parabola.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(\frac{2}{9}, \frac{8}{9})$

Let $A (t_{1}^{2}, 2 t_{1})$ and $B (t_{2}^{2}, 2 t_{2})$ be coordnates of the end points of a chord of the parabola $y^{2} = 4 x$ having slope 2.
Now, slope fo AB is ,
$m = \frac{2 t_{2} - 2 t_{1}}{t_{2}^{2} - t_{1}^{2}} = \frac{2 (t_{2} - t_{1})}{(t_{2} - t_{1}) (t_{2} + t_{1})} = \frac{2}{t_{2} + t_{1}}$
But m = 2
$\Rightarrow 2 = \frac{2}{t_{2} + t_{1}}$ ,
$\Rightarrow t_{1} + t_{2} = 1$
Let P (h,k) be a point on AB such that, it divides AB internally in the ratio 1 : 2.
Then, $h = \frac{2 t_{1}^{2} + t_{2}^{2}}{2 + 1}$ and $k = \frac{2 (2 t_{1}) + 2 t_{2}}{2 + 1}$ ,
$\Rightarrow 3 h = 2 t_{1}^{2} + t_{2}^{2}$ .....(ii)
and $3 k = 4 t_{1} + 2 t_{2}$ .....(iii)
On substituting value of $t_{1}$ from Eq. (i) Eq. (iii)
$3 k = 4 (1 - t_{2}) + 2 t_{2}$
$\Rightarrow 3 k = 4 - 2 t_{2}$
$\Rightarrow t_{2} = 2 - \frac{3 k}{2}$ .....(iv)
On substituting $t_{1} = 1 - t_{2}$ in Eq. (ii) we get
$3 h = 2 {(1 - t_{2})}_{2}^{2} + t_{2}^{2}$
$= 2 (1 - 2 t_{2} + t_{2}^{2}) + t_{2}^{2}$
$= 3 t_{2}^{2} - 4 t_{2} + 2 = 3 (t_{2}^{2} - \frac{4}{3} t_{2} + \frac{2}{3})$
$= 3 [{(t_{2} - \frac{2}{3})}_{2}^{2} + \frac{2}{3} - (\frac{4}{9}] = 3 {(t_{2} - \frac{2}{3})}_{2}^{2} + \frac{2}{3}$
$\Rightarrow 3 h - \frac{2}{3} = 3 {(t_{2} - \frac{2}{3})}_{2}^{2}$
$\Rightarrow 3 (h - \frac{2}{9}) = 3 {(2 - \frac{3 k}{2} - \frac{2}{3})}^{2}$ [from Eq. (iv)]
$\Rightarrow 3 (h - \frac{2}{9}) = 3 {(\frac{4}{3} - \frac{3 k}{2})}^{2}$
$\Rightarrow (h - \frac{2}{9}) \frac{9}{4} {(k - \frac{8}{9})}^{2}$
$\Rightarrow {(k - \frac{8}{9})}^{2} = \frac{4}{9} (h - \frac{2}{9})$
On generalising, we get the requried locus
${(y - \frac{8}{9})}^{2} = \frac{4}{9} (x - \frac{2}{9})$
This represents a parabola with vertex at $(\frac{2}{9}, \frac{8}{9})$

|

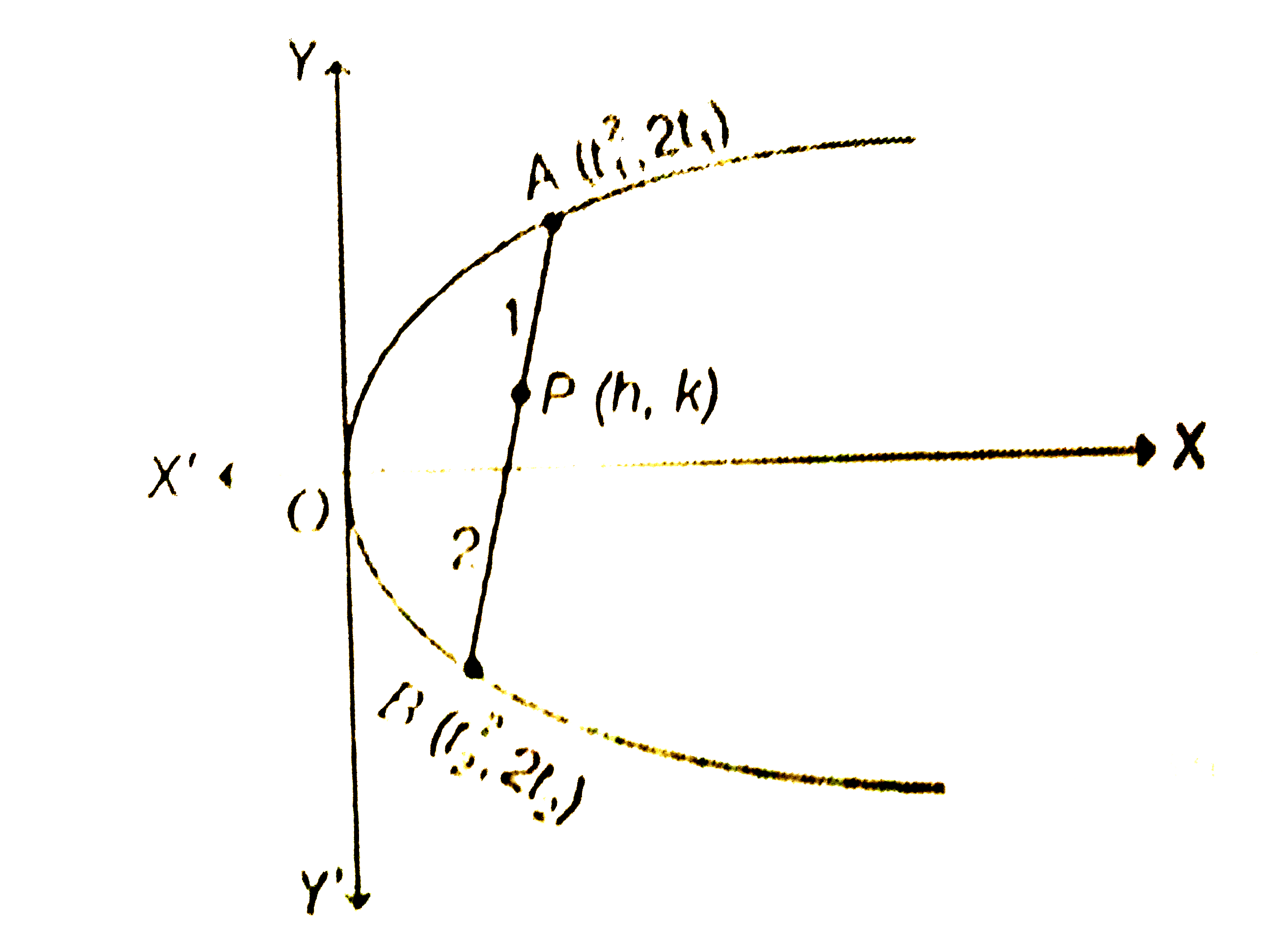
Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The locus of the middle points of the normal chords of the parabola, $y^{2} = 4 a x$ is
A $x + 2 a = \frac{y^{2}}{2 a} + \frac{4 a^{3}}{y^{2}}$
B $x + 2 a = \frac{y^{2}}{2 a} - \frac{4 a^{3}}{y^{2}}$
C $x - 2 a = \frac{y^{2}}{2 a} + \frac{4 a^{3}}{y^{2}}$
DNone of these
Question 2 - Select One
The locus of the middle points of the focal chord of the parabola $y^{2} a x$ , is
A $y^{2} = a (x - a)$
B $y^{2} = 2 a (x - a)$
C $y^{2} = 4 a (x - a)$
Dnone of these
Question 3 - Select One
Find the locus of the mid-points of the chords of the parabola $y^{2} = 4 a x$ which subtend a right angle at vertex of the parabola.
A $y^{2} = 2 a (x + 4 a)$
B $y^{2} = 2 a (x - 4 a)$
C $y^{2} = 0 (x - 2 a)$
D $y^{2} = a (x + 2 a)$

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )

Home
Ask Doubt
Profile