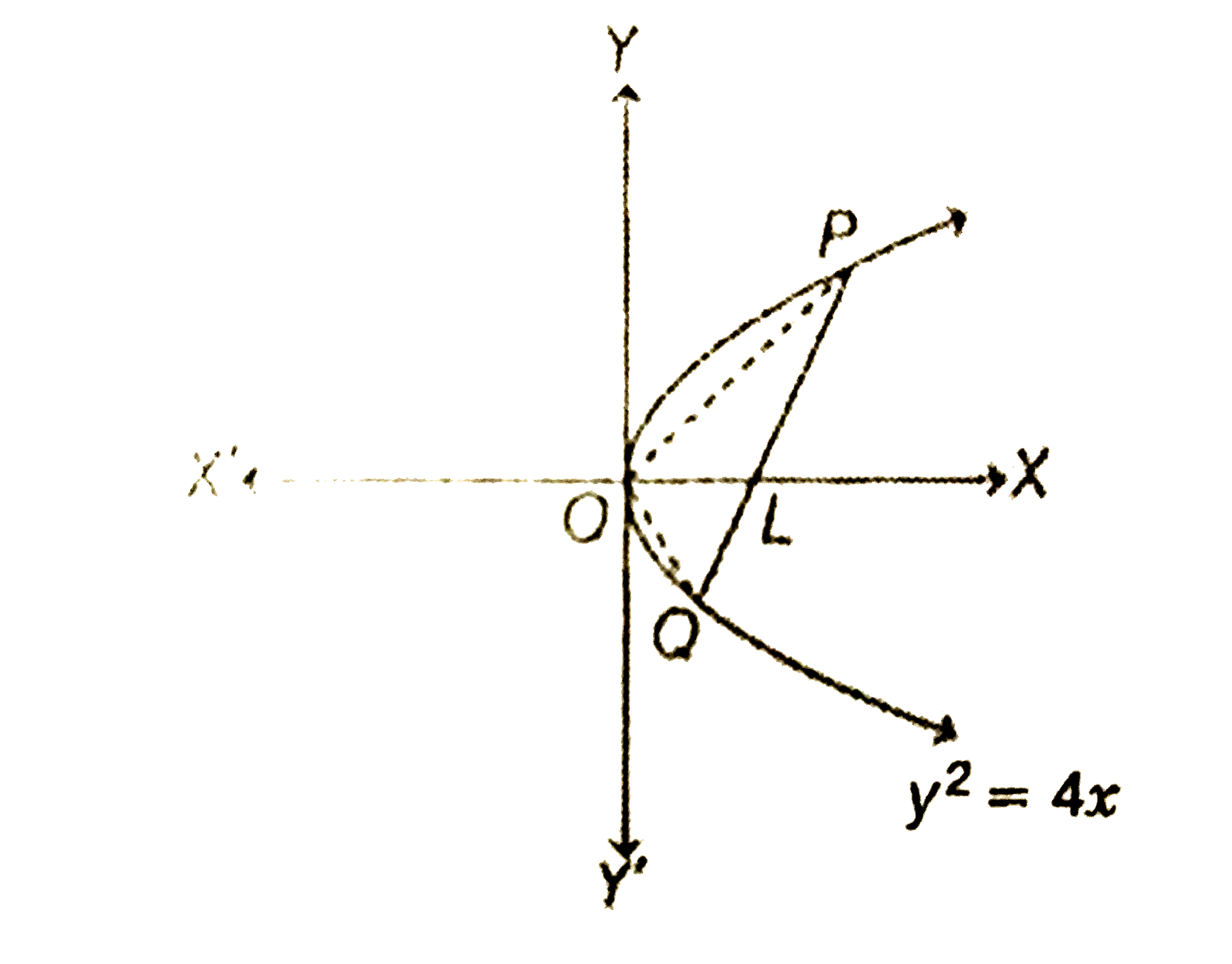
Through the vertex 'O' of parabola $y^{2} = 4 x$ , chords OP and OQ are drawn at right angles to one another. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the middle point of PQ.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $y^{2} = 2 (x - 4)$

Let the equation of chord OP be y = mx
Then, equation of chord will be $y = - \frac{1}{m} x$ and P is point of interection of y - mx and $y^{2} = 4 x$ is
$(\frac{4}{m^{2}}, \frac{4}{m})$ and Q is point intersection of $y = - \frac{1}{m} x$ and $y^{2} = 4 x$ is $(4 m^{2}, - 4 m)$
Now, equation of PQ is
$y + 4 m = \frac{\frac{4}{m} + 4 m}{\frac{4}{m^{2}} - 4 m^{2}} (x - 4 m^{2})$
$\Rightarrow y + 4 m = \frac{m}{1 - m^{2}} (x - 4 m^{2})$
$\Rightarrow (1 - m^{2}) y + 4 m - 4 m^{3} = m x - 4 m^{3}$
$\Rightarrow m x - (1 - m^{2}) y - 4 m = 0$
This line meets X-axis where y = 0
i.e., $x = 4 \Rightarrow O L = = 4$ which is costant as indepdedent of m.
Again let (h,k) be the mid-point of PQ. Then
$h = (4 m^{2} + \frac{4}{m^{2}} / (2)$
and $k \frac{\frac{4}{m} - 4 m}{2}$
$\Rightarrow h = 2 (m^{2} + \frac{1}{m^{2}})$
and $k = 2 (\frac{1}{m} - m)$
$\Rightarrow h = 2 [{(m - \frac{1}{m})}^{2} + 2]$
and $k = 2 (\frac{1}{m} - m)$
Eliminating m, we get
$2 h = k^{2} + 8$
or $y^{2} = 2 (x - 4)$ is required equation of locus

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Through the vertex O of a parabola $y^{2} = 4 x$ chords OP and OQ are drawn at right angles to one-another. Then for all positions of P, PQ cuts the axis of the parabola at a fixed point and the locus of the middle point of PQ is
A $y^{2} = 2 (x - 2)$
B $y^{2} = 2 (x - 4)$
C $y^{2} = 2 (x - 6)$
Dnone
Question 2 - Select One
Through the vertex O of a parabola $y^{2} = 4 x$ chords OP and OQ are drawn at right angles to one-another. Then for all positions of P, PQ cuts the axis of the parabola at a fixed point and the locus of the middle point of PQ is
A $y^{2} = 2 x + 8$
B $y^{2} = x + 8$
C $y^{2} = 2 x - 8$
D $y^{2} = x - 8$
Question 3 - Select One
Through the vertex of the parabola $y^{2} = 4 a x$ , chords OA and OB are drawn at right angles to each other . For all positions of the point A, the chord AB meets the axis of the parabola at a fixed point . Coordinates of the fixed point are :
A(a,0)
B(-a,0)
C(4a,0)
D(-4a,0)

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )

Home
Ask Doubt
Profile