A rod of length 13 metres has one end P on the X-axis and the other end Q on the y-axis. If P moves on the X-axis with a speed of 12 m/sec, then the speed of the other end Q when it is 12 m from the origin is
3 m/sec
5 m/sec
−5 m/sec
4 m/sec
The correct Answer is:C
To solve the problem, we need to analyze the situation involving a rod of length 13 meters with one end on the x-axis and the other on the y-axis. Let's denote the coordinates of point P on the x-axis as (x, 0) and point Q on the y-axis as (0, y).
1. Understanding the Geometry:
The length of the rod is constant and given as 13 meters. According to the Pythagorean theorem, we can express this relationship as:
x2+y2=132
or
x2+y2=169
2. Differentiating with Respect to Time:
To find the relationship between the rates of change of x and y, we differentiate both sides of the equation with respect to time t:
ddt(x2+y2)=ddt(169)
Using the chain rule, we get:
2xdxdt+2ydydt=0
Dividing through by 2 simplifies this to:
xdxdt+ydydt=0
3. Substituting Known Values:
We know that the speed of point P (which is moving along the x-axis) is given as:
dxdt=12 m/s
We need to find dydt when point Q is 12 meters from the origin, which means y=12.
4. Finding the Value of x:
We can substitute y=12 into the original equation to find x:
x2+122=169
This simplifies to:
x2+144=169
x2=169−144=25
Therefore, x=5.
5. Substituting into the Rate Equation:
Now we substitute x=5, y=12, and dxdt=12 into the differentiated equation:
5(12)+12dydt=0
This simplifies to:
60+12dydt=0
Rearranging gives:
12dydt=−60
Dividing both sides by 12 results in:
dydt=−5 m/s
Final Answer:
The speed of the other end Q when it is 12 m from the origin is −5 m/s.
The length of the rod is constant and given as 13 meters. According to the Pythagorean theorem, we can express this relationship as:
x2+y2=132
or
x2+y2=169
To find the relationship between the rates of change of x and y, we differentiate both sides of the equation with respect to time t:
ddt(x2+y2)=ddt(169)
Using the chain rule, we get:
2xdxdt+2ydydt=0
Dividing through by 2 simplifies this to:
xdxdt+ydydt=0
We know that the speed of point P (which is moving along the x-axis) is given as:
dxdt=12 m/s
We need to find dydt when point Q is 12 meters from the origin, which means y=12.
We can substitute y=12 into the original equation to find x:
x2+122=169
This simplifies to:
x2+144=169
x2=169−144=25
Therefore, x=5.
Now we substitute x=5, y=12, and dxdt=12 into the differentiated equation:
5(12)+12dydt=0
This simplifies to:
60+12dydt=0
Rearranging gives:
12dydt=−60
Dividing both sides by 12 results in:
dydt=−5 m/s
The speed of the other end Q when it is 12 m from the origin is −5 m/s.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - MTG-WBJEECHAPTER - APPLICATION OF DERIVATIVES EXERCISE - WB JEE WORKOUT ( CATEGORY3 : One or More than One Option Correct Type (2 Marks)
15 Videos
- APPLICATION OF DERIVATIVES BOOK - MTG-WBJEECHAPTER - APPLICATION OF DERIVATIVES EXERCISE - WB JEE Previous Years Questions ( CATEGORY 1: Single Option correct Type (1 Mark))
15 Videos
- APPLICATION OF DERIVATIVES BOOK - MTG-WBJEECHAPTER - APPLICATION OF DERIVATIVES EXERCISE - WB JEE Previous Years Questions ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
11 Videos
- A.P.,G.P.,H.P.BOOK - MTG-WBJEECHAPTER - A.P.,G.P.,H.P.EXERCISE - WB JEE Previous Years Questions ( CATEGORY 2 : Single Option Correct Type (2 Mark ) )
5 Videos
- APPLICATION OF INTEGRALSBOOK - MTG-WBJEECHAPTER - APPLICATION OF INTEGRALSEXERCISE - WE JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
3 Videos
Similar Questions
there is a bar of length a cm whose one end is on origin and other end is on the X-axis find Co ordinate of both the ends of the bar
View SolutionA rod of length 2 m is held vertically with one of its end on the floor. It is then allowed to fall. Calculate the speed of the other end when it strikes the floor. Assume that the end of the rod which is on the floor does not slip.
View Solution
Knowledge Check
From the origin at the same time two points being to move. The first moves on the X-axis at a speed =4 m/s, and the second on the Y axis at a spe3ed of 3 m/ sec.
AThe angular velocity of first wrt second is constantBThe velocity of separation of the two bodies is constantCThe velocity of separation of the two bodies after 2 sec is 5 m/sDThe angular velocity of first wrt second after 2 sec. is 5 rad/sIf one end of the diameter of a circle is (3, 4) which touches the x-axis then the locus of other end of the diameter of the circle is
AparabolaBhyperbolaCellipseDnone of theseThe distance of M(12,23) from the x-axis is :
A12 unitsB21 unitsC23 unitsD25 units
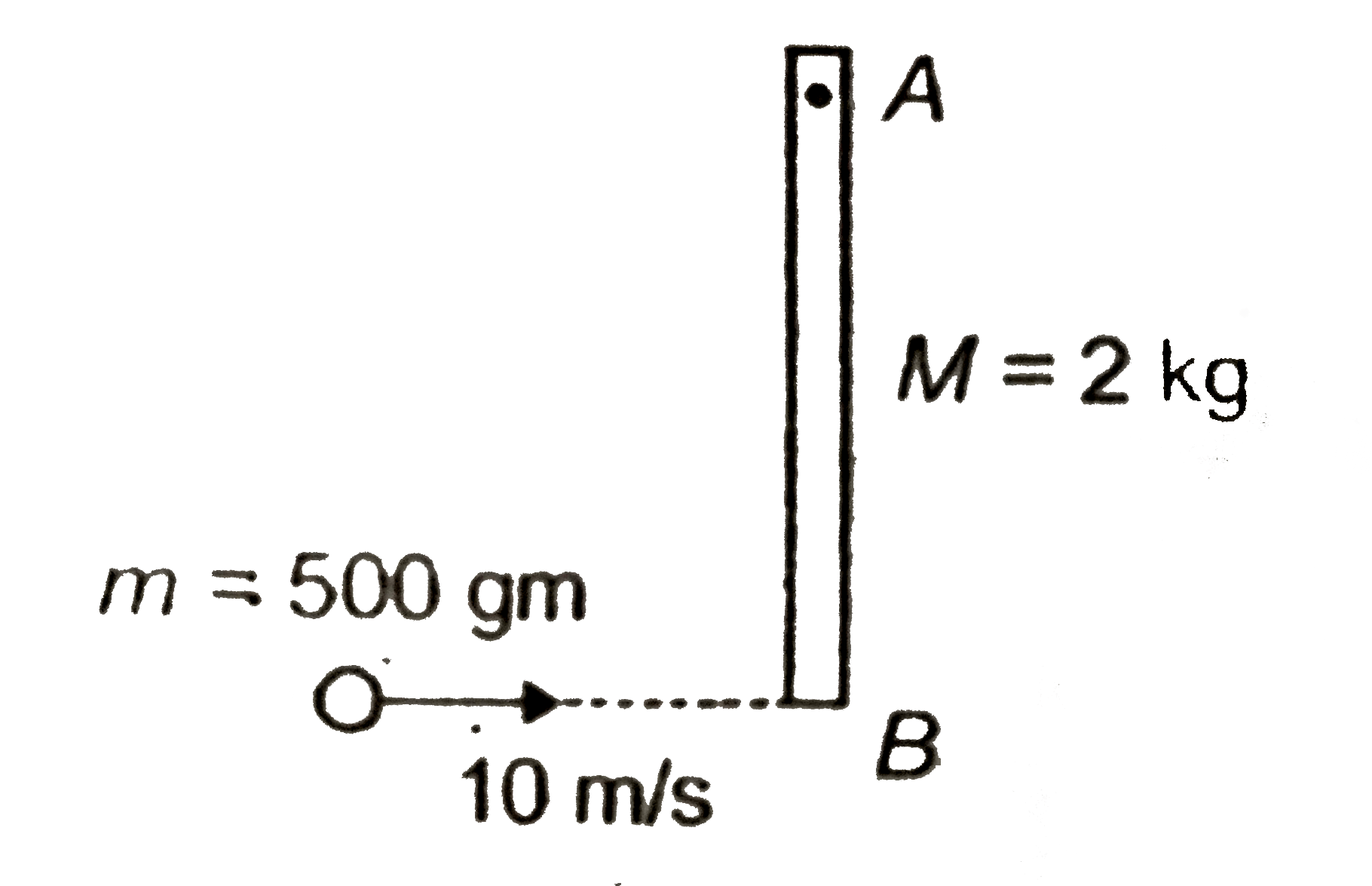
A rod of mass 2kg and length 1m is pivoted at one end A and kept on a smooth surface. A particle of mass 500gmstrikestheotherendB of the rod and sticks to the rod. If particle was moving with the speed of 20m/s, what is the angular speed of the rod after collision ?
View SolutionA uniform rod of mass M has an impulse applied at right angles to one end. If the other end begins to move with speed V, the magnitude of the impulse is
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?

View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionFrom the point (4, 3) a perpendicular is dropped on the x-axis well as on the y-axis. If the lengths of perpendiculars are p, q respectively, then which one of the following is correct ?
View Solution
