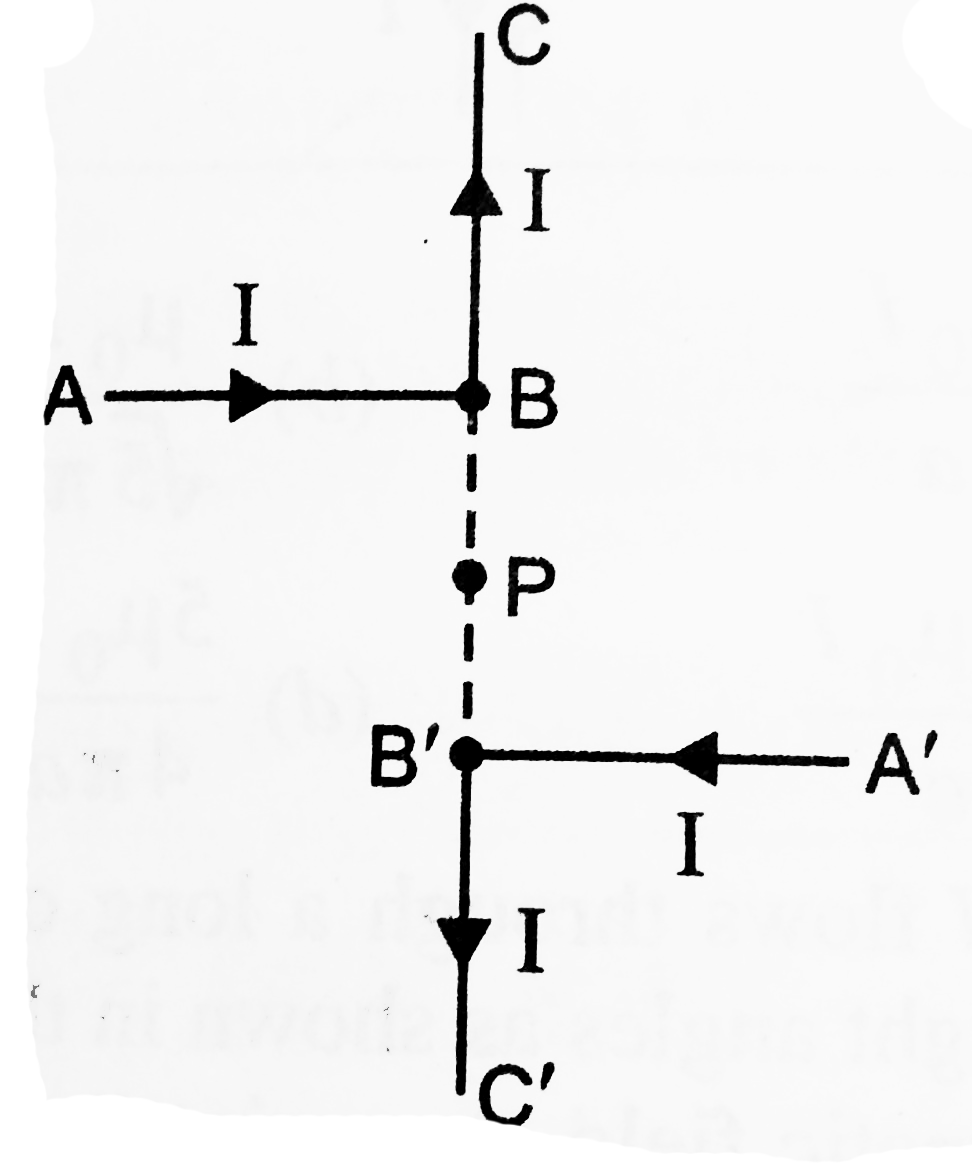
Current through ABC A'B'C' is I. What is the magnetic field at P? BP= PB' = r (Here C'B' PBC are collinear)

A

$B = \frac{1}{4 π} \frac{2 I}{r}$

B

$B = \frac{μ_{0}}{4 π} (\frac{2 I}{r})$

C

$B = \frac{μ_{0}}{4 π} (\frac{I}{r})$

D

zero

Text Solution

Verified by Experts

The correct Answer is:B

The magnetic field at point P due to current I in AB is
$B_{A B} = \frac{μ_{0}}{4 π} \frac{I}{r} O x$
The magnetic field at point P due to current I in BC is
$B_{B C} = 0$ (As the point P is along the BC). The magnetic field at point P due to current I in A.B. is
$B_{A . B .} = \frac{μ_{0}}{4 π} \frac{I}{r} \otimes$
The magnetic field at point P due to current I in B.C. is
$B_{B . C .} = 0$ (as the point P is along the BC)

$∴$ The net magnetic fieldat P is
$B = B_{A B} + B_{B C} + B_{A . B .} + B_{B . C .}$
$= \frac{μ_{0} I}{4 π r} + 0 + \frac{μ_{0} I}{4 π r} + 0 = 2 (\frac{μ_{0} I}{4 π r}) = \frac{μ_{0}}{4 π} (\frac{2 I}{r})$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Current through ABC and A'B'C' is 1. What is the magneticfield at P? BP=PB=r(henceC'B'andpbc are collinear)

A $B = \frac{1}{4 π} \frac{2 I}{r}$
B $B = \frac{μ_{0}}{4 π} (\frac{2 I}{r})$
C $B = \frac{μ_{0}}{4 π} (\frac{I}{r})$
Dzero
Question 2 - Select One
Currents through ABC and $A^{'} B^{'} C^{'}$ is I, figure. What is the magnetic field at P? $B P = P B^{'} = r$ . (Here $C^{'} B^{'} P B C$ are collinear)

A $\frac{2 I}{4 π r}$
B $\frac{μ_{0}}{4 π} (\frac{2 I}{r})$
C $\frac{μ_{0}}{4 π} (\frac{1}{r})$
Dzero
Question 3 - Select One
The magnetic field on the axis of a circular current carrying conductor of radius r at a distance r from centre is $B_{a}$ and the magnetic field at its centre is $B_{c}$ . The value of $B_{a} : B_{c}$ is
A $2 \sqrt{2} : 1$
B $\sqrt{2} : 1$
C $1 : 2 \sqrt{2}$
D $1 : \sqrt{2}$

MTG-WBJEE-MAGNETIC EFFECT OF CURRENT-WB JEE Previous Years Questions

Home
Ask Doubt
Profile