सत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक है :
(i) p(x)=3x+1,x=−13 (ii) p(x)=5x−π,x=45
(iii) p(x)=x2−1,x=1,−1 (iv) p(x)=(x+1)(x−2),x=−1,2
(v) p(x)=x2,x=0 (vi) p(x)=lx+m,x=−ml
(vii) p(x)=3x2−1,x=−1√3,2√3 (vii) p(x)=2x+1,x=12
The correct Answer is:(i) हाँ (ii) नहीं (iii) हाँ (iv) हाँ (v) हाँ (vi) हाँ
(vii) −1√3 बहुपद का एक शून्यक है, परन्तु 2√3 बहुपद का एक शून्यक नहीं है। (viii) नहीं
Step by step video, text & image solution for सत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक है : (i) p(x)=3x +1, x= -(1)/(3) " (ii) " p(x) =5x-pi, x =(4)/(5) (iii) p(x)=x^(2)-1, x =1, -1 " (iv) " p(x)=(x+1)(x-2), x= -1,2 (v) p(x)=x^(2), x =0 " (vi) "p(x)=l x+m, x= -(m)/(l) (vii) p(x) =3x^(2)-1, x = -(1)/(sqrt(3)), (2)/(sqrt(3)) " (vii) " p(x)=2x+1, x=(1)/(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NCERT HINDICHAPTER - बहुपदEXERCISE - प्रश्नावली 2.35videos
बहुपद
- BOOK - NCERT HINDICHAPTER - बहुपदEXERCISE - प्रश्नावली 2.45videos
बहुपद
- BOOK - NCERT HINDICHAPTER - बहुपदEXERCISE - प्रश्नावली 2.11videos
बहुपद
- BOOK - NCERT HINDICHAPTER - प्रायिकता EXERCISE - प्रश्नावली 15.25videos
प्रायिकता
- BOOK - NCERT HINDICHAPTER - रचनाएंEXERCISE - प्रश्नावली 11.214videos
रचनाएं
Similar Questions
विभाजन एल्गोरिथ्म का प्रयोग करके , निम्न में P(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
(i)p(x)=x3−3x2+5x−3,g(x)=x2−2
(ii)p(x)=x4−3x2+4x+5 ,g(x)=x2+1−x
(iii)p(x)=x4−5x+6. , g(x)=2−x208:03View Solutionसत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याऍं उसकी शून्यक हैं। तथा शुन्यांको और गुणांको के बीच के संबंध को भी सत्यापित कीजिए
(1) 2x3+x2−5x+2, 1/2,1,−2
(2) x3−4x2+5x−2, 2,1,105:22View Solutionकिसी बहुपद p(x) के लिए y=p(x) का ग्राफ नीचे 2.10 में दिया है । प्रत्येक स्थिति में p(x) के शून्यको की संख्या ज्ञात कीजिए ।
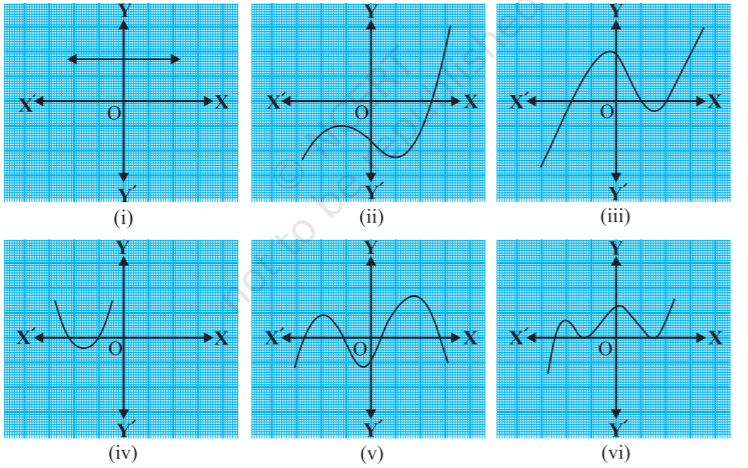 04:26View Solution
04:26View Solutionदो ग्राहक श्याम और एकता एक विशेष दुकान पर एक ही सप्ताह में जा रहे है (मंगलवार से शनिवार तक) प्रत्येक द्वारा दुकान पर किसी दिन या किसी अन्य दिन जाने के परिणाम समप्रायिक है। इसकी क्या प्रायिकता है की दोनों उस दुकान पर (i) एक ही दिन जाएँगे? (ii) क्रमागत दिनों में जाएँगे? (iii) भिन्न-भिन्न दिनों में जाएँगे।
09:22View Solution6cm त्रिज्या का एक वृत्त खींचिए। केंद्र से 10cm दूर स्थित एक बिंदु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लंबाइयां मापिए।
View SolutionVerify whether the following are zeroes of the polynomial, indicated against them.(i) p(x)=3x+1,x=−13 (ii) p(x)=5x−π,x=45 (iii) p(x)=x2−1,x=1,−1(iv) p(x)=(x+1)(x+2),x=−1,2 (v) p(x)=x2,x=0 (vi) p(x)=lx+m,x=−ml
05:40View Solutionसत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक है :
(i) p(x)=3x+1,x=−13
(ii) p(x)=5x,πx=45
(iii) p(x)=x2−1,x=1,−1
(iv) p(x)=(x+1)(x−2),x=−1,2
(v) p(x)=x2,x=0
(vi) p(x)=lx+m,x=−ml
(vii) p(x)=3x2−1,x=−1√3,2√3
(viii) p(x)=2x+1,x=1204:03View Solutionसत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक है :
(i) p(x)=3x+1,x=−13
(ii) p(x)=5x−π,x=45
(iii) p(x)=x2−1,x=1,−1
(iv) p(x)=(x+1)(x−2),x=−1,2
(v) p(x)=x2,x=0
(vi) p(x)=lx+m,x=−ml
(vii) p(x)=3x2−1,x=−1√3,2√3
(viii) p(x)=2x+1,x=12View SolutionVerify whether the following are zeroes of the polynomial, indicated against them .
(i) p(x)=3x+1,x=−13
(ii) p(x)=5x−π,x=45
(iii) p(x)=x2−1,x=1,−1
(iv) p(x)=(x+1)(x−2),x=−1,2
(v) p(x)=x2,x=0
(vi) p(x)=lx+m,x=−ml
(vii) p(x)=3x2−1,x=−1√3,2√3
(viii) p(x)=2x+1,x=1205:23View Solutionसत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक है :
(i) p(x)=3x+1,x=13
(ii) p(x)=5x−π,x=45
(iii) p(x)=x2−1,x=1,−1
(iv) p(x)=(x+1)(x−2),x=1=−1,2
(v) p(x)=x2,x=0
(vi) p(x)=lx+m,x=−ml
(vii) p(x)=3x2−1x=−1√x,2√3
(viii) p(x)=2x+1,x=1203:03View SolutionVerify whether the values of x given in each case are the zeroes of the polynomial or not ?
(i) p(x)=2x+1,x=−12
(ii) p(x)=5x−π,x=−32
(iii) p(x)=x2−1,x=±1
(iv) p(x)=(x−1)(x+2),x=−1,−2
(v) p(y)=y2,y=0
(vi ) p(x)=ax+b,x=−ba
(vii) f(x)=3x2−1,x=−1√3,2√3
(viii) f(x)=2x−1,x=12,−1203:56View SolutionVerify whether the values of x given in each case are the zeroes of the polynomial or not ?
(i) p(x)=2x+1,x=−12
(ii) p(x)=5x−π,x=−32
(iii) p(x)=x2−1,x=±1
(iv) p(x)=(x−1)(x+2),x=−1,k−2
(v) p(y)=y2,y=0
(vi ) p(x)=ax+b,x=−ba
(vii) f(x)=3x2−1,x=−1√3,2√3
(viii) f(x)=2x−1,x=12,−1205:55View SolutionVerify whether the values of x given in each case are the zeroes of the polynomial or not ?
(i) p(x)=2x+1,x=−12
(ii) p(x)=5x−π,x=−32
(iii) p(x)=x2−1,x=±1
(iv) p(x)=(x−1)(x+2),x=−1,k−2
(v) p(y)=y2,y=0
(vi ) p(x)=ax+b,x=−ba
(vii) f(x)=3x2−1,x=−1√3,2√3
(viii) f(x)=2x−1,x=12,−1207:24View SolutionCheck whether the given value of the variable is zero of the corresponding polynomial (i) p(x)=x^(2)-1,x=1-1 (Ii) p(x)=5x-pi,x=4/5 (iii) p(x)=lx+m,x=(-m)/(l) (iv) p(x)=(x+1)(x-2),x=-1,2 (v)p(x)=3x^(2)-1,x=(-1)/sqrt(3),(2)/sqrt(3)
04:32View SolutionFind the value of p (0), p (-1) and p (3) for each of the polynomials given below. (i) p(x)=x^(2)-3x (ii) p(x)=x^(3)+1 (iii) p(x)=(x-1)(x-2) (iv) p(x)=3x^(2)-2x+3
02:02View Solution

