A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.
 Solution in Telugu
Solution in Telugu
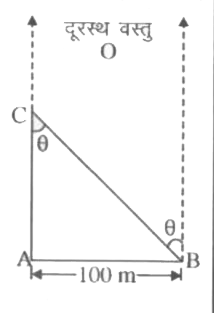
We have, parallax angle θ=40∘ From fig.2.3. AB=AC tanθ
AC=AB/tanθ = 100m/tan40∘=100m/0.8391=119
Topper's Solved these Questions
- BOOK - NCERT TELUGUCHAPTER - UNITS AND MEASUREMENTEXERCISE - Exercise (Fill in the blanks)8videos
UNITS AND MEASUREMENT
- BOOK - NCERT TELUGUCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE26videos
UNITS AND MEASUREMENT
- BOOK - NCERT TELUGUCHAPTER - THERMODYNAMICS EXERCISE - EXERCISES10videos
THERMODYNAMICS
- BOOK - NCERT TELUGUCHAPTER - WAVESEXERCISE - Exercises21videos
WAVES
Similar Questions
The volume of a cube of side 1 cm is equal to …….m3.
06:36View Solution1 calorie=4.2 J where IJ= 1 kg m2s−2. Suppose we employ a system of units in which the unit of mass is α kg, the unit of length is β m and the unit of time γs, show that a calorie has a magnitude 4.2α−1β−2γ−2 in the new system.
02:43View SolutionA geyser heats water flowing at the rate of 3.0 litres per minute from 27°C to 77°C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4.0×104J/g ?
06:36View SolutionA steel wire has a length of 12.0m and a mass of 2.10kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20∘C=343ms−1
02:12View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle theta = 40^@ ( theta "is known as parallax"). Estimate the distance fo the tower C from his original position A.
03:28View Solutionकिसी टावर के पाद से 160 मी . दूर स्थित बिंदु से टावर का उन्नयन कोंढ टावर के पाद की ओर 100 मी . दूरी चलने पर दो गुना हो जाता है । टावर की ऊंचाई ज्ञात करे ।
View Solutionएक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी का आकलन करना चाहता है । वह मीनार C के सामने किसी बिंदु A पर खड़ा होता है और AC की सीध में बहुत दूर स्थित किसी बिंदु O को देखता है । फिर वह, AC के लंबवत 100 m दूर स्थित बिंदु B तक चलता है और वहाँ से O एवं C को फिर देखता है । क्योंकि O बहुत अधिक दूरी पर है , BO एवं AO की दिशाएँ व्यावहारिक रूप में एक ही हैं, लेकिन वह पाता है कि C की दृष्टि रेखा मूल दृष्टि रेखा के सापेक्ष θ=40∘ पर घूम गई है (θ को लम्बन कहा जाता है ) उसकी मूल स्थिति A से मीनार C की दूरी का आकलन कीजिए ।
05:54View Solutionएक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी आकलन करना चाहता है। वह मीनार C के सामने किसी बिंदु A पर खड़ा होता है और AC की सीध में बहुत दूर स्थित किसी बिंदु O को देखता है। फिर वह AC के लंबवत 100 m दूर स्थित बिंदु B तक चलता है। और वहाँ से O एवं C को फिर देखता है। क्योंकि O बहुत अधिक दूरी पर है, BO एवं AO की दिशाएँ व्यावहारिक रूप में एक ही हैं, लेकिन वह पता है कि C की दृष्टि रेखा मूल दृष्टि रेखा के सापेक्ष θ=40∘ पर घूम गई है। (θ को लंबवत कहा जाता है ) उसकी मूल स्थिति A से मीनार C की दूरी का आकलन कीजिए।
 02:39View Solution
02:39View SolutionA man standing at a point P is watching the top of elevation of 30∘. The man walks some distance towards the tower and then his angle of elevation of thetop of the toweris 60∘. If the height of the tower 30 m, then the distance he moves is
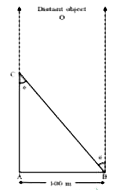
02:39View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant , the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘ (θ is known as 'Parallax') estimate the distance of the tower C from his original position A.
 02:42View Solution
02:42View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant , the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle theta = 40^(@) ( theta is known as 'Parallax') estimate the distance of the tower C from his original position A.
01:59View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.
 04:26View Solution
04:26View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.
 02:39View Solution
02:39View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘(θ is known as parallax). Estimate the distance fo the tower C from his original position A.
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in fron of the tower C and spots a very distant objct O in line with AC. He then walks pependicular to AC up to B, a distance of 100 m and look at O and C again. Since O is very distant the direction BO is practivally the same as AO, but he finds the line of slight by of C shifted fro the original line of slight by an angle θ=30∘(θ is known as parallax) estimate the distance of the tower C from his original position A.
View Solutionमीनार के आधार से क्षैतिज रेखा में स्थित किसी बिंदु से मीनार के शिखर का उन्नयन कोण 30∘ देखा गया । जब प्रेक्षक मीनार की ओर 100 मी. चलता है तो वह पाता है कि शिखर का उन्नयन कोण 60∘ हो गया है । मीनार की ऊँचाई और प्रथम स्थिति से मीनार की दूरी ज्ञात कीजिए ।
00:51View Solution

