Suppose the frequency of the source in the previous example can be varied. (a) What is the frequency of the source at which resonance occurs? (b) Calculate the impedance, the current, and the power dissipated at the resonant condition.
(a) The frequency at which the resonance occurs is
ω0=1√LC=1√25.48×10−3×796×10−6
=222.1rad/s
vr=ω02π=221.12×3.14Hz=35.4Hz
(b) The impedance Z at resonant condition is equal to the resistance:
Z=R=3Ω
The rms current at resonance is
=VZ=VR=(283√2)13=66.7A
The power dissipated at resonance is
=P=I2×R=(66.7)2×3=13.35kW
You can see that in the present case, power dissipated at resonance is more than the power dissipated in Example 7.8.
Similar Questions
Suppose the frequency of the source in the above example can be varied (a) What is the frequency of the source at which resonance occurs ? (b) Calculate the impedeance, the current and power dissipated at the resonant condition.
View SolutionSuppose the frequency of the source in the above example can be varied (a) What is the frequency of the source at which resonance occurs ? (b) Calculate the impedeance, the current and power dissipated at the resonant condition.
View Solution
Knowledge Check
In a series R-L-C circuit, the frequency of the source is half of the resonance frequency. The nature of the circuit will be
AcapacitiveBinductiveCpurely resistiveDdata unsufficient
What happens to the impedance and current amplitude at resonant frequency ?
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.
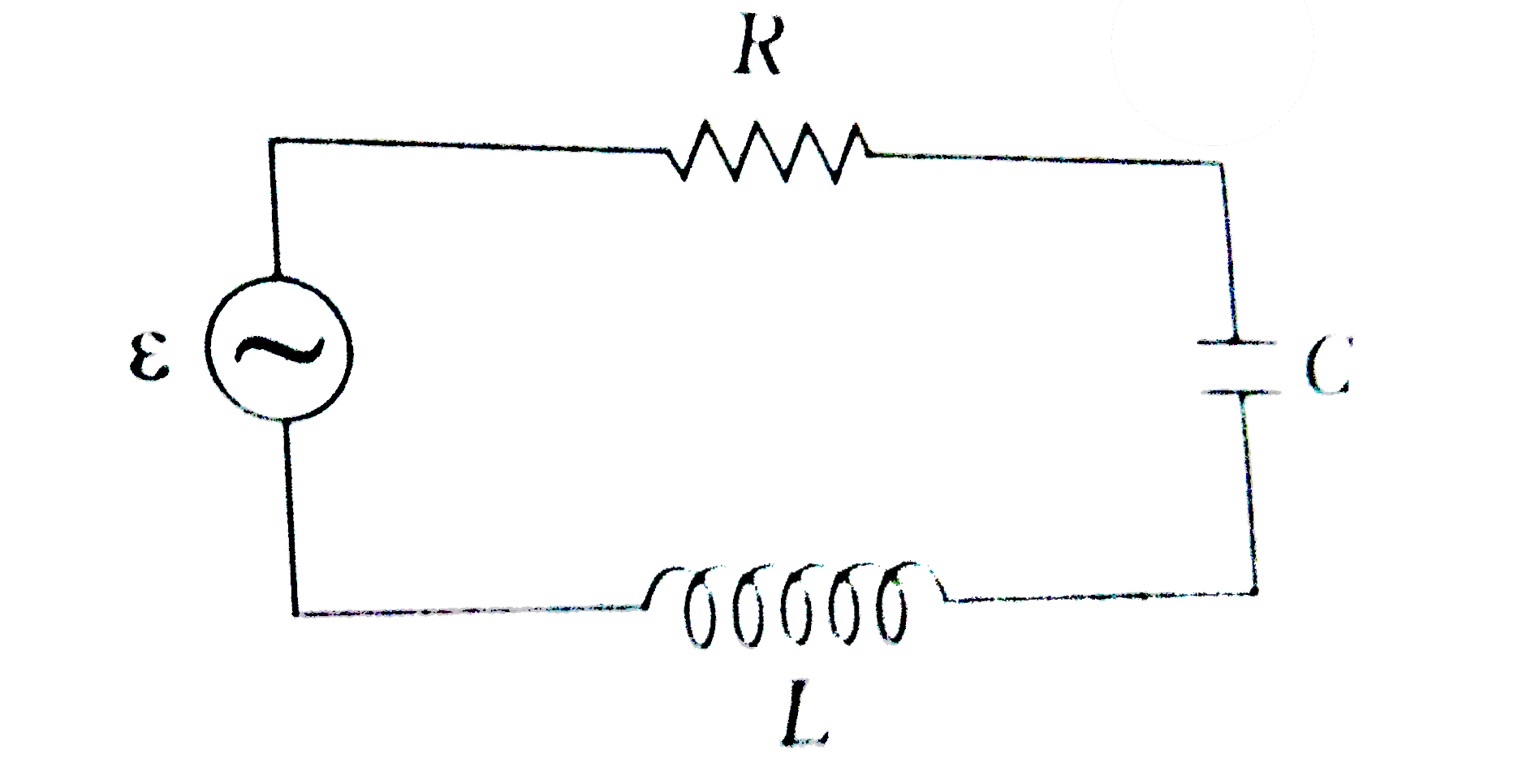
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.
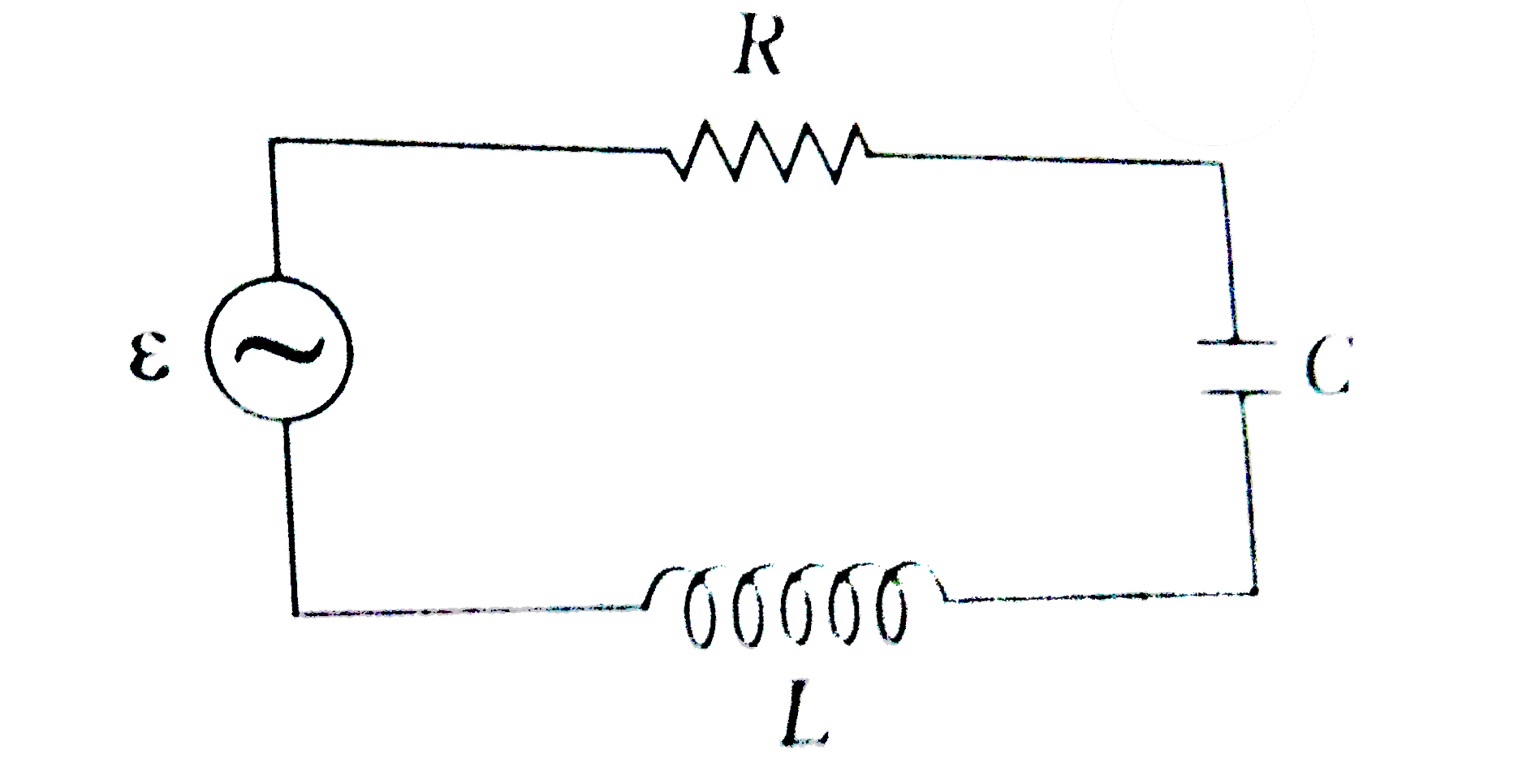
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionWhen the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero. Does it mean that there is no current through the inductor or the capacitor?
View SolutionWhen the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero. Does it mean that there is no current through the inductor or the capacitor?
View Solution
