Two identical small charged spheres, each having a mass m, hang in equilibrium the length of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
To solve the problem of finding the magnitude of the charge on each of the two identical small charged spheres hanging in equilibrium, we can follow these steps:
Step 1: Understand the Setup
We have two identical small charged spheres, each with mass m, hanging from strings of length l. The strings make an angle θ with the vertical. The spheres are charged and repel each other due to electrostatic forces.
Step 2: Identify Forces Acting on the Spheres
Each sphere experiences three forces:
1. The gravitational force acting downward: Fg=mg
2. The tension in the string T, which can be resolved into two components:
- Tcosθ acting vertically upward
- Tsinθ acting horizontally (away from the other sphere)
3. The electrostatic repulsive force Fe between the two charged spheres.
Step 3: Set Up Equilibrium Conditions
Since the spheres are in equilibrium:
- In the vertical direction (y-direction):
Tcosθ=mg(1)
- In the horizontal direction (x-direction):
Fe=Tsinθ(2)
Step 4: Calculate the Electrostatic Force
The electrostatic force Fe between two charges q separated by a distance r is given by Coulomb's law:
Fe=14πϵ0q2r2
The distance r between the two spheres can be calculated as:
r=2lsinθ
Thus,
Fe=14πϵ0q2(2lsinθ)2=14πϵ0q24l2sin2θ=q216πϵ0l2sin2θ
Step 5: Substitute Fe into the Equilibrium Conditions
From equation (2):
q216πϵ0l2sin2θ=Tsinθ
From equation (1), we can express T:
T=mgcosθ
Substituting T into the horizontal force equation:
q216πϵ0l2sin2θ=mgcosθsinθ
Step 6: Rearranging the Equation
Rearranging gives:
q2=16πϵ0l2sin2θ⋅mgsinθcosθ
This simplifies to:
q2=16πϵ0l2mgsin3θcosθ
Step 7: Solve for q
Taking the square root to find q:
q=√16πϵ0l2mgsin3θcosθ=4l√πϵ0mgsin3θcosθ
Final Answer
The magnitude of the charge on each sphere is:
q=4l√πϵ0mgsin3θcosθ
---
We have two identical small charged spheres, each with mass m, hanging from strings of length l. The strings make an angle θ with the vertical. The spheres are charged and repel each other due to electrostatic forces.
Each sphere experiences three forces:
1. The gravitational force acting downward: Fg=mg
2. The tension in the string T, which can be resolved into two components:
- Tcosθ acting vertically upward
- Tsinθ acting horizontally (away from the other sphere)
3. The electrostatic repulsive force Fe between the two charged spheres.
Since the spheres are in equilibrium:
- In the vertical direction (y-direction):
Tcosθ=mg(1)
- In the horizontal direction (x-direction):
Fe=Tsinθ(2)
The electrostatic force Fe between two charges q separated by a distance r is given by Coulomb's law:
Fe=14πϵ0q2r2
The distance r between the two spheres can be calculated as:
r=2lsinθ
Thus,
Fe=14πϵ0q2(2lsinθ)2=14πϵ0q24l2sin2θ=q216πϵ0l2sin2θ
From equation (2):
q216πϵ0l2sin2θ=Tsinθ
From equation (1), we can express T:
T=mgcosθ
Substituting T into the horizontal force equation:
q216πϵ0l2sin2θ=mgcosθsinθ
Rearranging gives:
q2=16πϵ0l2sin2θ⋅mgsinθcosθ
This simplifies to:
q2=16πϵ0l2mgsin3θcosθ
Taking the square root to find q:
q=√16πϵ0l2mgsin3θcosθ=4l√πϵ0mgsin3θcosθ
The magnitude of the charge on each sphere is:
q=4l√πϵ0mgsin3θcosθ
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionTwo vectors having equal magnitudes A make an angle θ with each other. Find the magnitude and direction of the resultant.
View SolutionA simple pendulum having a bob of mass m under goes small oscillations with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
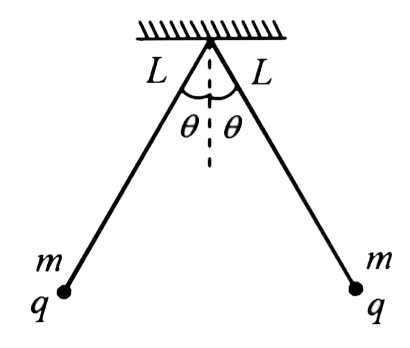
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
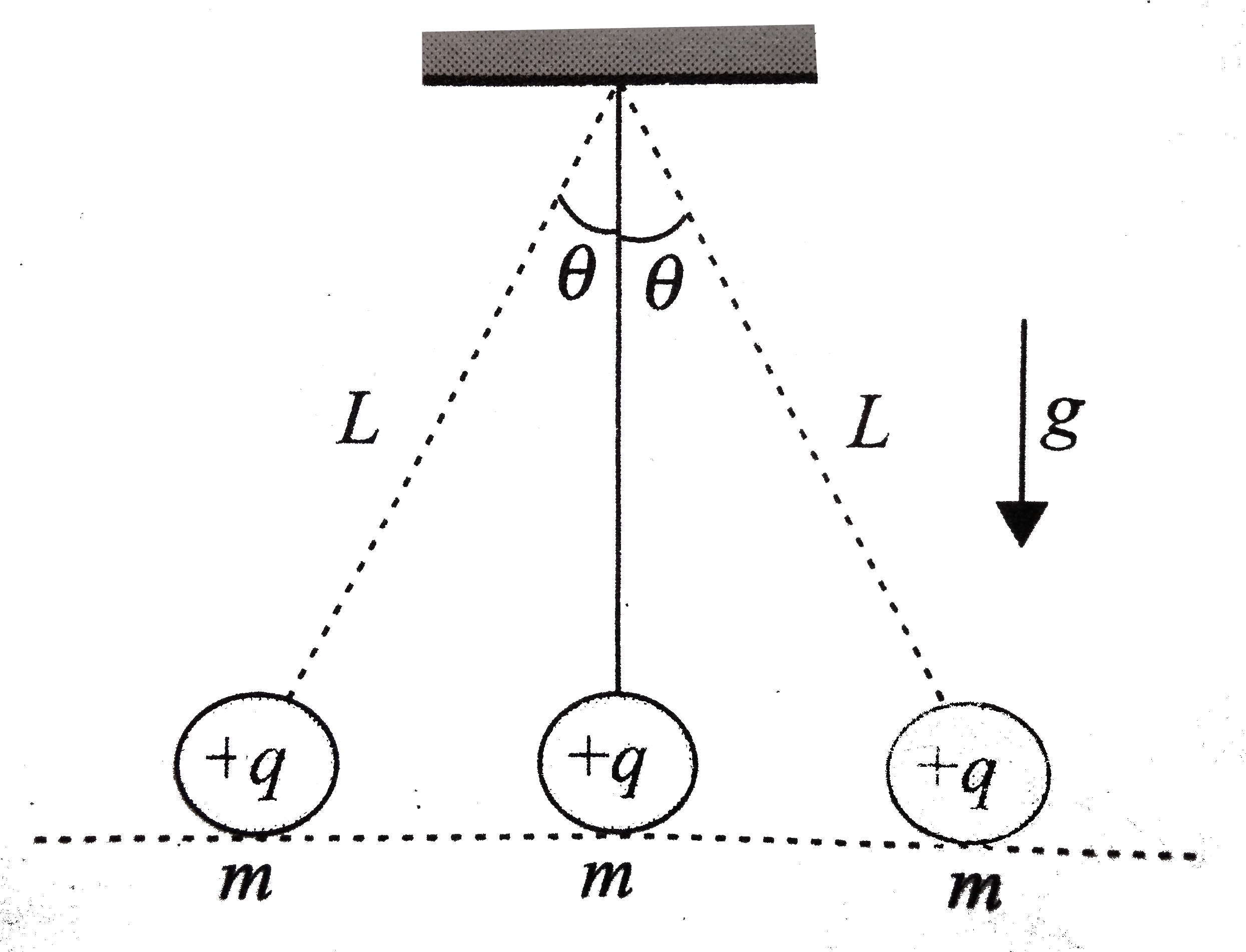
View SolutionThree identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View Solution
