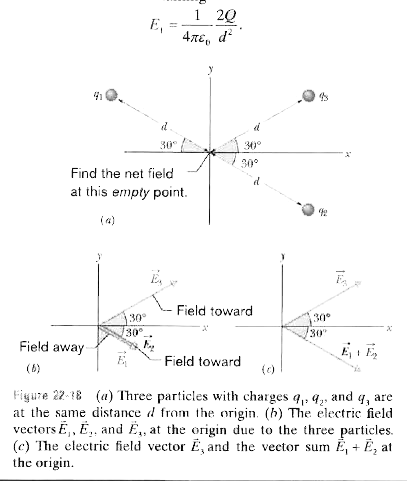
Figure 22-18a shows there particles with charges q1=+2Q,q2=−2Q,andq3=−2Q, each a distance d from the origin. What net electric field →E is produced at the origin?
KEY IDEAS
Charges q1,q2,andq3 produce electric field vectors →E1,→E2and→E3, respectively, at the origin, and the net electric field is the vector sum →E=→E1+→E2+→E3. To find this sum, we first must find the magnitudes and orientations of the three field vectors.
Magnitudes and directions: To find the magnitude of →E1, which is due to q1, we use Eq. 20-20, substituting d for r and 2Q for q and obtaining E1=14πε02Qd2.
Similarly, we find the magnitudes of →E2and→E3 to be
E2=14πε02Qd2andE3=14πε04Qd2.
We next must find the orientations of the three electric field vectors at the origin. Because q1 is a positive charge, the field vector it produces points directly away from it, and because q2andq3 are both negative, the field vectors they produce point directly toward each of them. Thus, the three electric fields produced at the origin by the three charged particles are oriented as in Fig. 22-18b.
Adding the fields: We can now add the fields vectorially just as we add force vectors. However, here we can use symmetry to simplify the procedure. From Fig. 22-18b, we see that electric fields →E1and→E2 have the same direction. Hence, their vector sum has that direction and has the magnitude
E1+E2=14πε02Qd2+14πε02Qd2=14πε04Qd2,
which happens to equal the magnitude of field →E3.
We must now combine two vectors, →E3 and the vector sum →E1+→E2, that have the same magnitude and that are oriented symmetrically about the x axis, as shown in Fig. 22-18c. From the symmetry of Fig. 22-18c, we realize that the equal y components of our two vectors cancel (one is upward and the other is downward and the equal x components add (both are rightward). Thus, the net electric field →E at the origin is in the positive direction of the x axis and has the magnitude
E=2E3x=2E3cos30∘
=(2)14πε04Qd2(0.866)=6.93Q4πε0d2. (Answer)
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Video
Similar Questions
Knowledge Check
Two points charges q and -2q are placed some distance d apart. If the electric field at the location of q is E, that at the location of -2q is
A−E2B−2ECE2D−4EThe point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
A−3E2B−EC−E2D−2E
In Fig., the four particles form a square of edge length a = 5.00 cm and have charges q1=+3nC,q2=−15nC,q3=+15nC, and q4=−30nC. In unit-vector notation, what net electric field do the particles produce at the square's center ?

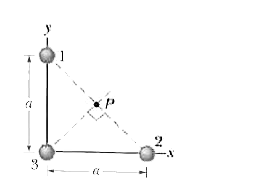
View SolutionIn Fig., the three particles are fixed in place and have charges q1=q2=+5e and q3=+2e. Distance a=3.00μm. What are the (a) magnitude and (b) direction of the net electric field at point P due to the particles ?
View SolutionIn Fig. four particles form a square. The charges are q1=q4=Q and q2=q3=q. (a) What is Q/q is the net electrostatic force on particles 2 and 3 is zero ? (b) Is there any value of q makes the net electrostatic force on each of the four particles zero ? Explain.

View SolutionThe point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View Solution