Figure 22-26a shows a plastic rod with a uniform charge -Q. It is bent in a 120∘ circular arc of radius r and symmetrically paced across an x axis with the origin at the center of curvature P of the rod. In terms of Q and r, what is the electric field →E due to the rod at point P?
KEY IDEAS
Because the rod has a continuous charge distribution, we must find an expression for the electric fields due to differential elements of the rod and then sun those fields via calculus.
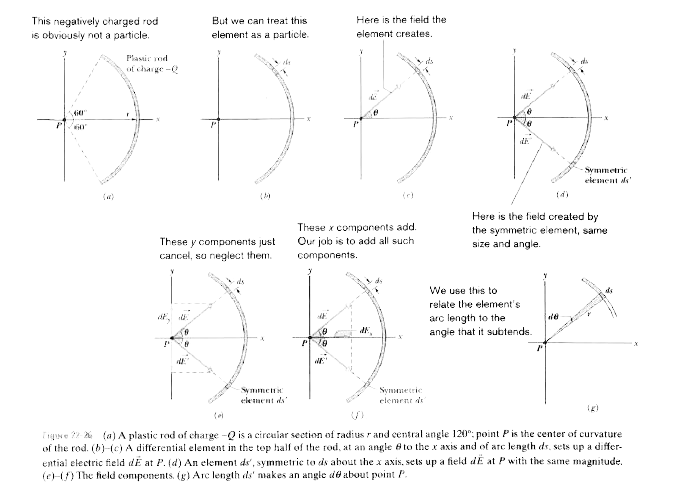
An element : Consider a differential element having arc length ds and located at an angle θ above the x axis (Figs. 22-26b and c). IF we let λ represent the linear charge density of the rod, our element ds has a differential charge of magnitude
dq=λds. (22−35)
The element.s field: Our element produces a differential electric field d→E at point P, which is a distance r from the element. Treating the element as a point charge, we can rewrite Eq. 22-3 to express the magnitude of d→E as
dE=14π∈0dqr2=14π∈0λdsr2. (22−36)
The direction of d→E is toward ds because charge dq is negative.
Symmetric partner: Our element has a symmetrically located (mirror image) element ds. in the bottom half of the rod. The electric field d→E. set up at P by ds. also has the magnitude given by Eq. 22-36, but the field vector points toward ds. as shown in Fig. 22-26d. If we resolve the electric field vectors of ds and ds. into x and y components as shown in Figs. 22-26e and f, we see that their y components cancel (because they have equal magnitudes and are in opposite directions). We also see that their x components have equal magnitudes and are in the same direction.
Summing: Thus, to find the electric field set up by the rod, we nened sum (via integration) only the x components of the differential electric fields set up by all the differential elements of the rod. From Fig. 22-26f and Eq. 22-36, we can write the component dEx set up by ds as
dEx=dEcosθ=14πε0λr2cosθds. (22−37)
Equation 22-37 has two variables, θ and s. Before we can integrate it, we must eliminate one variable. We do so by replacing ds, using the relation
ds=rdθ,
in which dθ is the angle at P that includes are length ds (Fig. 22-26g). With this replacement, we can integrate Eq. 22-37 over the angle made by the rod at P, from θ=−60∘ to θ=60∘, that will give us the field magnitude at P:
E=∫dEx=∫60∘−60∘14πε0λr2cosθrdθ
=λ4πε0r∫60∘−60∘cosθdθ=λ4πε0r[sinθ]60∘−60∘
=λ4πε0r[sin60∘−sin(−60∘)]=1.73λ4πε0r. (22−38)
(If we had reversed the limits on the integration, we would have gotten the same result but with a minus sign. Since the integration gives only the magnitude of →E, we would then have discarded the minus sign.)
Charge density: To evaluate λ, we note that the full rod subtends an angle of 120∘ and so is one-third of a full circle. It arc length is then 2πr/3, and its linear charge density must be
λ=chargelength=Q2πr/3=0.477Qr
Substituting this into Eq. 22-23 and simplifying give us
E=(1.73)(0.477Q)4πε0r2=0.83Q4πε0r2. (Answer)
The direction of →E is toward the rod, along the axis of symmetry of the charge distribution. We can write →E in unit-vector notation as
→E=0.83Q4πε0r2ˆi.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
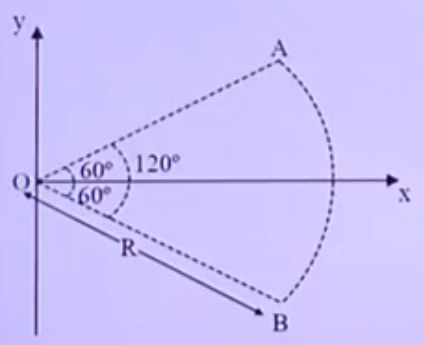
Figure shows a rod AB, which is bent in a 120∘ circular arc of radius R. A charge (-Q) is uniformly distributed over rod AB. What is the electric field →E at the centre of curvature O ?
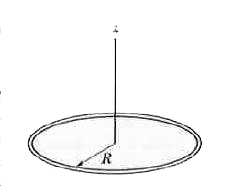
View SolutionA thin nonconducting rod with a uniform distribution of positive charge Q is bent into a complete circle of radius R (Fig.). The central perpendicular axis through the ring is a z aaxis, with the origin at the center of the ring. What is the magnitude of the electric field due to the rod at (a) z = 0 and (b) z=∞ ? (c ) In terms of R, at what positive and Q=5.00μC, what is the maximum magnitude ?
View Solution
Knowledge Check
(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
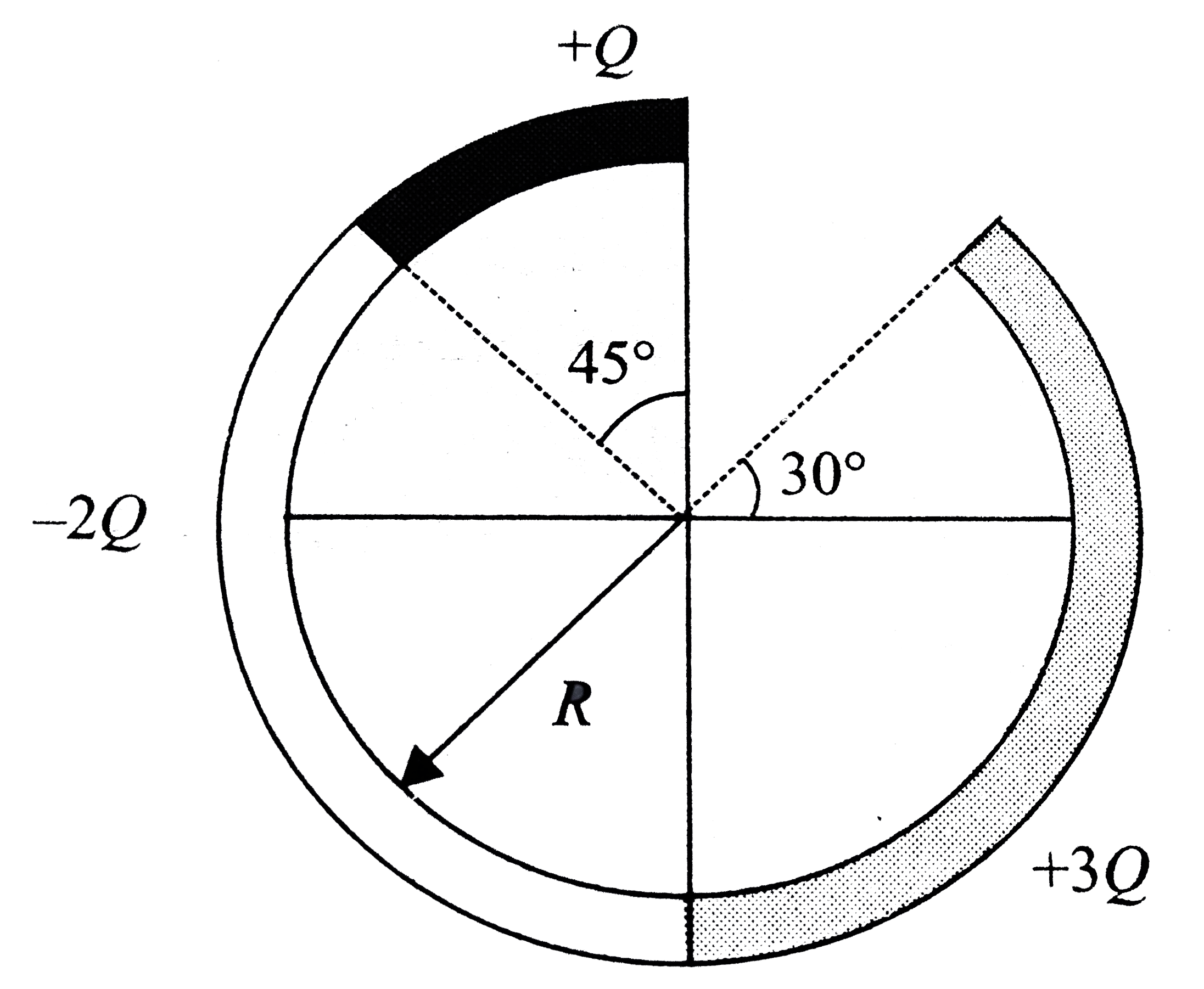 .Aq2πε0RB5Q12πε0RC3Q32πε0RDnone of these.
.Aq2πε0RB5Q12πε0RC3Q32πε0RDnone of these.(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
 .AQ2πε0RBQ4πε0RC2Qπε0RDQπε0R
.AQ2πε0RBQ4πε0RC2Qπε0RDQπε0RA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
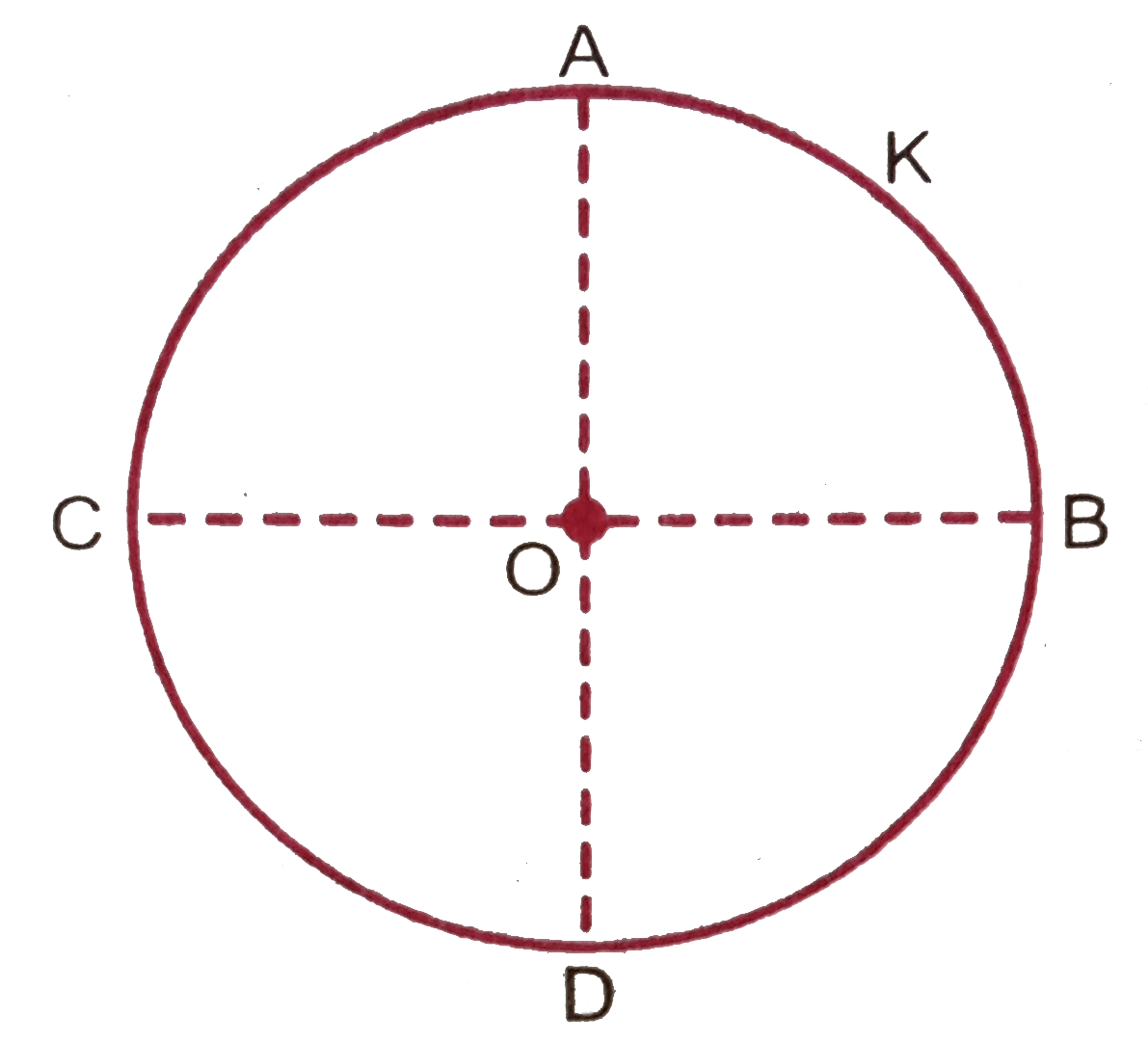 A3E along KOBE along OKCE along KOD3E along OK
A3E along KOBE along OKCE along KOD3E along OK
(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
 .
.
View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is λ. Find the electric field due to the rod at a point P which is at a distance r from the rod.
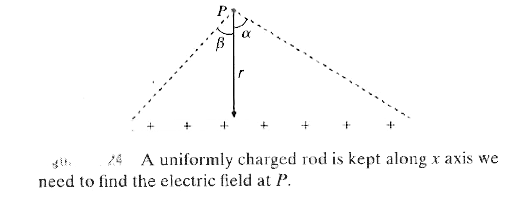
View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is

View SolutionA rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
View SolutionA rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
View Solution
