Figure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is . Find the electric field due to the rod at a point P which is at a distance r from the rod.
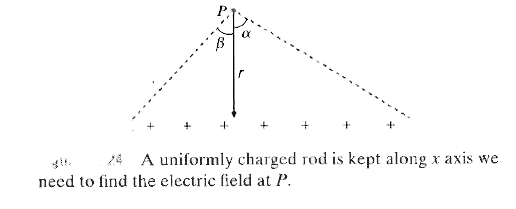
KEY IDEA
Because the rod has a continuous charge distribution, we must find an expression for the electric fields due to differential elements of the rod and then sum those fields via calculus.
Calculations : An element : Consider a differential element having length dx. If the length of a line segment is dx, the charge on it is . Here is the charge per unit length of the line (assumed to be constant).
Thus,
.
The element.s field: Our element produces a differential electric field. Treating this element as a point charge, the electric field due to this small charge at a distance r from the line is
.
The electric field is away from the charge because the charge is positive .
Summing: Thus, to find the electric field set up by the rod, we need sum (via integration) the parallel as well as perpendicular components of the differential electric field is setup by all the differential elements of the rod.
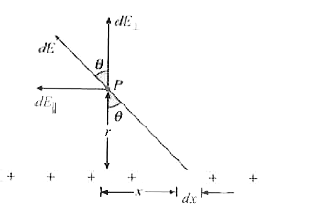
Let us resolve this electric field in a direction parallel and perpendicular to the line charge.
,
,
.
From the geometry of Fig. 22-25, we can say that
,
.
Since we need to replace x everywhere by the variable , we need to differentiate this expression with respect to .
,
.
By replacing this expression for dE, we get
,
,
.
Similarly resolving the electric field in the perpendicular direction, we have
Note: If the line is infinite which means that it extends from to , we can assume .
Then
.
If the line is semi-infinite, extending from to the foot of the perpendicular, we can assume .
Then
.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
A rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric field at a point P located along the long axis of the rod and at a distance a from one end

View SolutionA thin straight rod of length 2a carrying a uniformly distributed charge q is located in vacumm. Find the magnitude of the electric field strength as a function of the distatance r from the rod's centre along the streaight line
(a) perpendicular to the rod and passing through its centre ,
(b) coinciding with the rod's direction (at the point lying outside the rod).
View Solution
Knowledge Check
A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
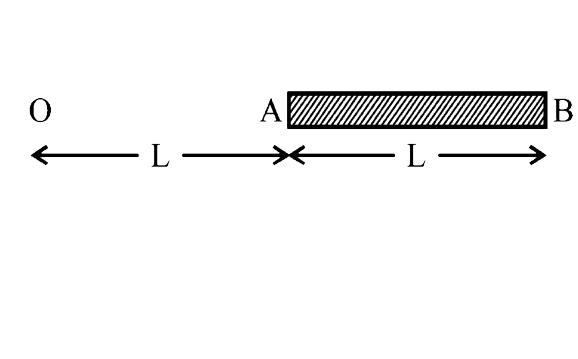 A(a) Q8πε0LB(b) 3Q4πε0LC(c) Q4πε0L1n2D(d) Q1n24πε0Ls
A(a) Q8πε0LB(b) 3Q4πε0LC(c) Q4πε0L1n2D(d) Q1n24πε0Ls
A rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric foeld at a point P located along the long axis of the rod and at a distance a from one end

View SolutionA rod of length 20 cm carries a charge of +150 μC that is uniformly distributed along its length. Find the electric field intensity at a point, which is 20 cm away from both the ends of the rod.
View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is

View SolutionA rod length l is uniformly charged with charge q. Calculate potential at point P.

View SolutionA rod length l is uniformly charged with charge q. Calculate potential at point P.

View Solution
