At what distance along the central perpendicular axis of a uniformly charged plastic disk of radius 0.600 m is the magnitude of the electric field equal to 25% of the magnitude of the field at the center of the surface of the disk ?
To solve the problem, we need to find the distance x along the central perpendicular axis of a uniformly charged plastic disk where the electric field is equal to 25% of the electric field at the center of the disk.
1. Identify the Given Values:
- Radius of the disk, R=0.600m
- Electric field at the center of the disk, EC
- We need to find the distance x where the electric field Ex=14EC.
2. Electric Field at the Center:
The electric field at the center of the disk is given by the formula:
EC=2kπσ
where k is Coulomb's constant and σ is the surface charge density.
3. Electric Field at a Distance x:
The electric field at a distance x along the axis of the disk is given by:
Ex=2kπσ(1−x√x2+R2)
4. Set Up the Equation:
We know that Ex=14EC. Therefore, we can write:
2kπσ(1−x√x2+R2)=14(2kπσ)
This simplifies to:
1−x√x2+R2=14
5. Rearranging the Equation:
Rearranging the equation gives:
x√x2+R2=1−14=34
6. Cross-Multiplying:
Cross-multiplying gives:
4x=3√x2+R2
7. Squaring Both Sides:
Squaring both sides results in:
16x2=9(x2+R2)
8. Expanding and Rearranging:
Expanding and rearranging gives:
16x2=9x2+9R2⟹7x2=9R2
9. Substituting the Value of R:
Substitute R=0.600m:
7x2=9(0.600)2
7x2=9×0.36=3.24
x2=3.247≈0.462857
10. Taking the Square Root:
Taking the square root gives:
x≈√0.462857≈0.680m
Final Answer:
The distance x along the central perpendicular axis where the electric field is equal to 25% of the electric field at the center of the disk is approximately 0.680m.
- Radius of the disk, R=0.600m
- Electric field at the center of the disk, EC
- We need to find the distance x where the electric field Ex=14EC.
The electric field at the center of the disk is given by the formula:
EC=2kπσ
where k is Coulomb's constant and σ is the surface charge density.
The electric field at a distance x along the axis of the disk is given by:
Ex=2kπσ(1−x√x2+R2)
We know that Ex=14EC. Therefore, we can write:
2kπσ(1−x√x2+R2)=14(2kπσ)
This simplifies to:
1−x√x2+R2=14
Rearranging the equation gives:
x√x2+R2=1−14=34
Cross-multiplying gives:
4x=3√x2+R2
Squaring both sides results in:
16x2=9(x2+R2)
Expanding and rearranging gives:
16x2=9x2+9R2⟹7x2=9R2
Substitute R=0.600m:
7x2=9(0.600)2
7x2=9×0.36=3.24
x2=3.247≈0.462857
Taking the square root gives:
x≈√0.462857≈0.680m
The distance x along the central perpendicular axis where the electric field is equal to 25% of the electric field at the center of the disk is approximately 0.680m.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
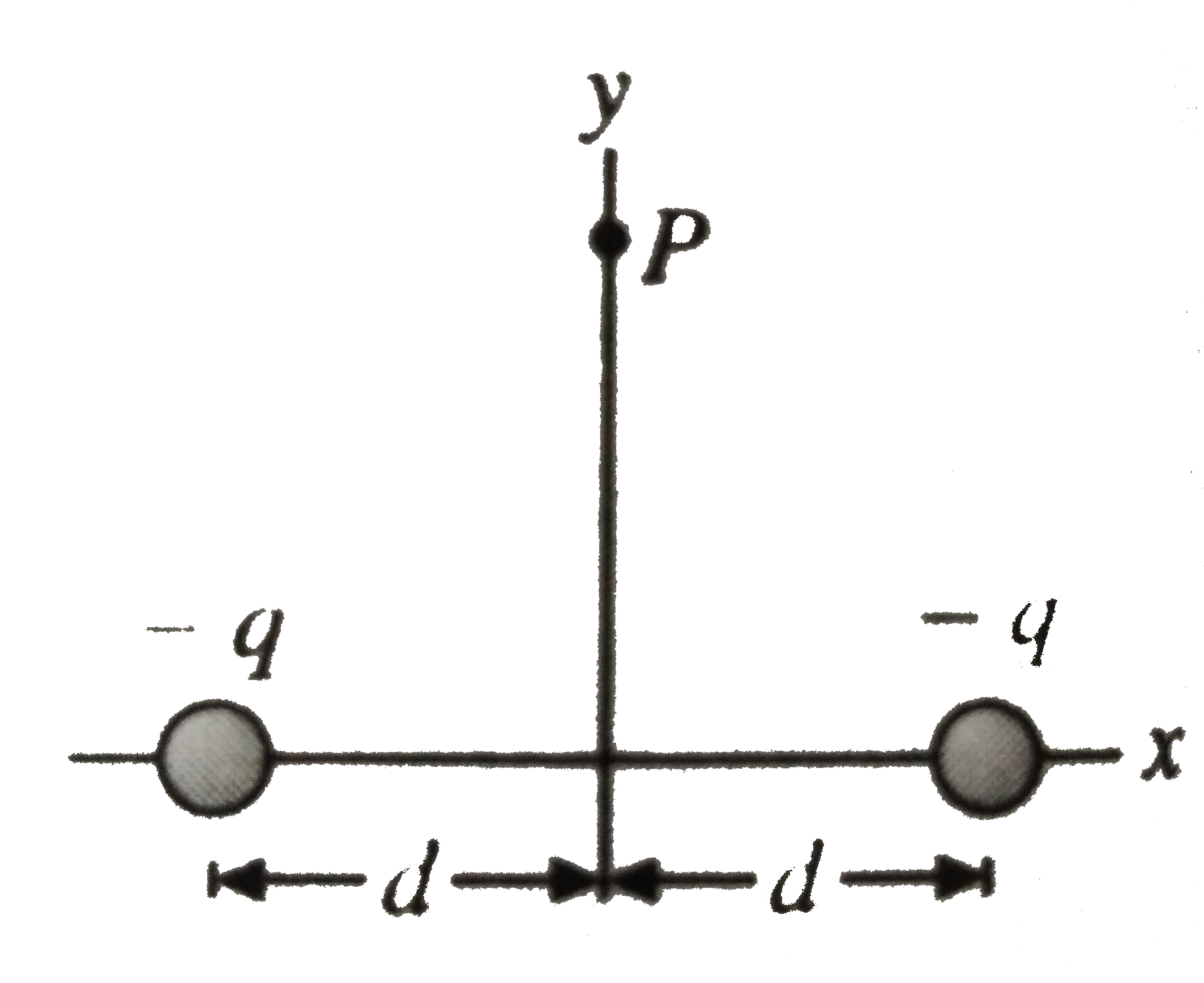
In fig, two particles, each of charge -q are arranged symmetrically about the y-axis, each producing an electric field at point P on the y-axis.
 .
.
(a) Are the magnitudes of the fields at P equal?
(b) Is each electric field directed towards or away form the charge producing it ?
(c ) Is the magnitude of the net electric field at P equal to the sum of the magnitudes E of the two field vectors (is it equal to 2E)?
(d) Do the x-components of those two field vectors add or cancel?
(e ) Do their y-components add or cancel?
(f) Is the diretion of the net field at P that of the canceling components or the adding components?
(g) What is the direction of the net field?
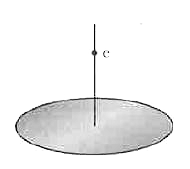
View SolutionIn Fig. an electron (e) is to be released from rest on the central axis of a uniformly charged disk of radius R. The surface charge density on the disk is +5.00μC/m2. What is the magnitude of the electron's initial acceleration if it is released at a distance (a) R, (b) R/100, and (c ) R/1000 from the center of the disk ? (d) Why does the acceleration magnitude increase only slightly as the release point is moved closer to the disk ?
View Solution
Knowledge Check
At which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?
AR√2BR√3C√2RD√3RThe surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc is σ2∈o. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc reduces by
Areduces by 70.7%Breduces by 29.3%Creduces by 9.7%Dreduces by 14.6%A sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
A1B2C4D8
For a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionFor a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionIf the potential at the center of a uniformly charged sphere of radius R is V then electric field at a distance r from the center of sphere will be (r<R) : -
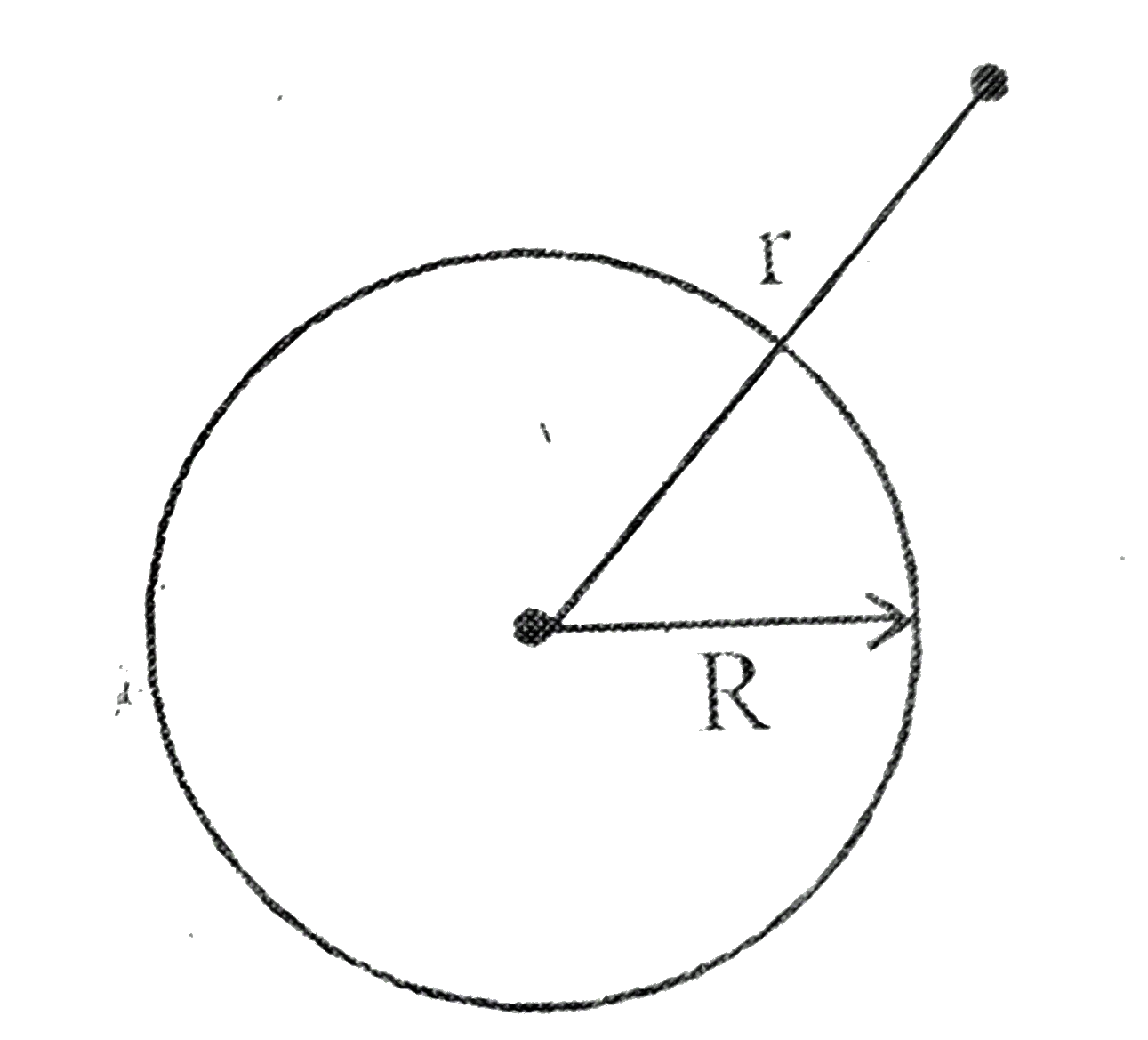
View SolutionA thin half ring of radius R=20cm is uniformly charged with a total charge q=0.70nC.Find the magnitude of the electric field strength at the curvaite centre of this half-ring.
View SolutionThe maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View Solution
