A plate carries a charge of −3.0μC, while a rod carries a charge of +2.0μC. How many electrons must be transferred from the plate to the rod, so that both objects have the same charge ?
6.3×1012 electrons
1.2×1013 electrons
8.0×1012 electrons
1.6×1013 electrons
The correct Answer is:D
To solve the problem of how many electrons must be transferred from the plate to the rod so that both objects have the same charge, we can follow these steps:
Step 1: Identify the initial charges
- The charge on the plate is Qp=−3.0μC (microcoulombs).
- The charge on the rod is Qr=+2.0μC.
Step 2: Define the final charge condition
We want both the plate and the rod to have the same charge after transferring some electrons. Let the number of electrons transferred be n.
Step 3: Calculate the charge of the transferred electrons
The charge of one electron is approximately −1.6×10−19C. Therefore, the total charge of n electrons is:
Qe=n×(−1.6×10−19C)
Step 4: Write the equations for final charges
After transferring n electrons from the plate to the rod:
- The new charge on the plate will be:
Q′p=Qp+Qe=−3.0μC+n×1.6×10−19C
- The new charge on the rod will be:
Q′r=Qr+Qe=+2.0μC+n×(−1.6×10−19C)
Step 5: Set the final charges equal
To find n, we set the final charges equal:
Q′p=Q′r
Substituting the expressions from step 4:
−3.0μC+n×1.6×10−19=+2.0μC−n×1.6×10−19
Step 6: Solve for n
Rearranging the equation gives:
n×1.6×10−19+n×1.6×10−19=+2.0μC+3.0μC
2n×1.6×10−19=5.0μC
Convert 5.0μC to coulombs:
5.0μC=5.0×10−6C
Now, substituting:
2n×1.6×10−19=5.0×10−6
n=5.0×10−62×1.6×10−19
Calculating n:
n=5.0×10−63.2×10−19≈1.5625×1013
Step 7: Round to the nearest whole number
Since we cannot transfer a fraction of an electron, we round n to the nearest whole number:
n≈15625×109 electrons
Final Answer
Approximately 15625 electrons must be transferred from the plate to the rod.
---
- The charge on the plate is Qp=−3.0μC (microcoulombs).
- The charge on the rod is Qr=+2.0μC.
We want both the plate and the rod to have the same charge after transferring some electrons. Let the number of electrons transferred be n.
The charge of one electron is approximately −1.6×10−19C. Therefore, the total charge of n electrons is:
Qe=n×(−1.6×10−19C)
After transferring n electrons from the plate to the rod:
- The new charge on the plate will be:
Q′p=Qp+Qe=−3.0μC+n×1.6×10−19C
- The new charge on the rod will be:
Q′r=Qr+Qe=+2.0μC+n×(−1.6×10−19C)
To find n, we set the final charges equal:
Q′p=Q′r
Substituting the expressions from step 4:
−3.0μC+n×1.6×10−19=+2.0μC−n×1.6×10−19
Rearranging the equation gives:
n×1.6×10−19+n×1.6×10−19=+2.0μC+3.0μC
2n×1.6×10−19=5.0μC
Convert 5.0μC to coulombs:
5.0μC=5.0×10−6C
Now, substituting:
2n×1.6×10−19=5.0×10−6
n=5.0×10−62×1.6×10−19
Calculating n:
n=5.0×10−63.2×10−19≈1.5625×1013
Since we cannot transfer a fraction of an electron, we round n to the nearest whole number:
n≈15625×109 electrons
Approximately 15625 electrons must be transferred from the plate to the rod.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Linked Comprehension)5videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems63videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
Similar Questions
Knowledge Check
- Question 1 - Select One
Two bodies X and Y carry charges −6.6μC and −5μC. How many electrons should be transferred from X to Y so that they acquire equal charges?
A2X1012B5X1013C5X1012D2X1013 - Question 2 - Select One
An aluminium nail has an excess charge of +3.2μC. How many electrons must be added to the nail to make it electrically neutral ?
A2.0×1013B3.2×1016C2.0×1019D3.2×106 - Question 3 - Select One
A 80 pF capacitor is charged to 15 V by connecting it to a battery. How many electrons are transferred from one plate to another?
A7.5×109B6×109C5×108D9×108
A thin metal plate of length 25 cm and breadth 4 cm in air carries a charge of 10μC. Calculate the outward pull on one side of the plate.
View SolutionA square of side d, made from a thin insulating plate, is uniformly charged and carries a total charge of Q. A point charge q is placed on the symmetrical normal axis of the square at a distance d/2 from the plate. How large is the force acting on the point charge ?
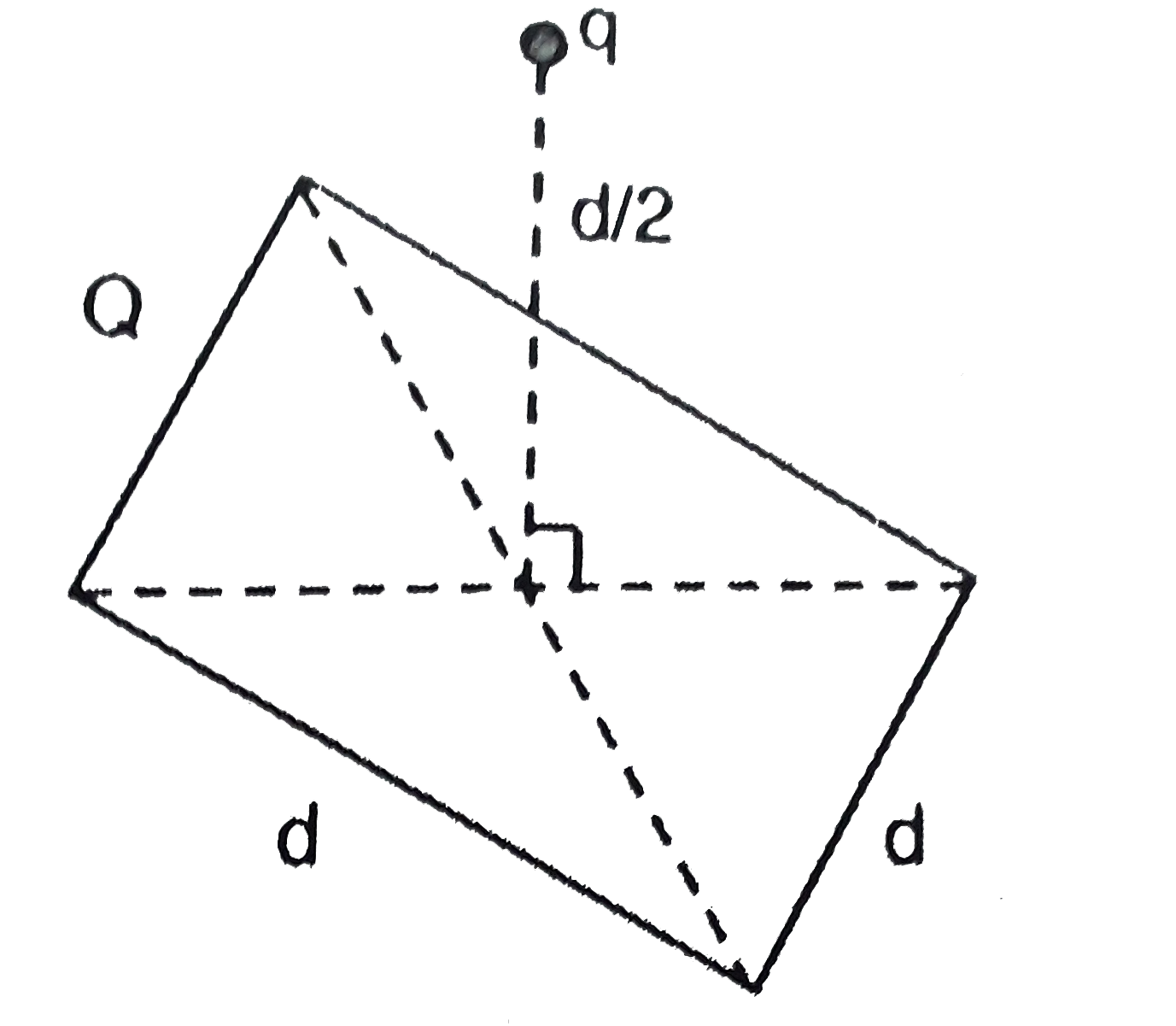 View Solution
View SolutionConsider three identical metal spheres, A, B and C. Sphere A carries of −2.0μC, spheres B carries a charge of −6.0μC, and spheres C carries a charge of +5.0μC. Sphere A and B are touched together and then separated. Sphere B and C are then touched and separated. Does sphere C end up with an excess or a deficiency of electrons and how many electrons is it ?
View SolutionA charge of 10μC lies at the centre of a square. Work done in carrying a charge of 2μC from one corner of square to the diagonally opposite corner is
View SolutionA metal plate of area 0.5 m2 is given a charge of 50μC, what is the charge density ?
View Solution

