A venturi meter is used to measure the flow speed of a fluid in a pipe . The meter is connected between two sections of the pipe (Fig) the cross-sectional area A of the entrance and exit of the meter matches the pipe's cross-sectional area a with speed v . A manometer connects the wider portion of the meter to the narrower portion . The change in the fluid's speed is accompanied by a change Δp in the fluid 's pressure , which causes a height difference h of the liquid in the two arms of the manometer. (Here , Δp means pressure in the throat minus pressure in the pipe).
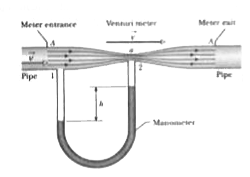
(a) By applying Bernoulli's equation and the equation of continuity to points 1 and 2 in Fig show that
V=√2a2Δpρ(a2−A2)
where r is the density of the fluid .
The continuity equation yields AV = av , and Bernoulli.s equation yields Δp+1/2ρV2=1/2ρV2 , where Δp=p1−p2 . The first equation gives v = (A/a) V . We use this to substitute for v in the second equation and obtain Δp+1/2ρV2=1/2ρ(A/a)2V . We solve this equation for V , to get
V=√2Δpρ(A/a)2−1=√2a2Δpρ(A2−a2)
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.26
1 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.27
1 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.24
1 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
A venturi meter is used to measure the flow speed of a fluid in a pipe . The meter is connected between two sections of the pipe (Fig) the cross-sectional area A of the entrance and exit of the meter matches the pipe's cross-sectional area a with speed v . A manometer connects the wider portion of the meter to the narrower portion . The change in the fluid's speed is accompanied by a change Δp in the fluid 's pressure , which causes a height difference h of the liquid in the two arms of the manometer. (Here , Δp means pressure in the throat minus pressure in the pipe).
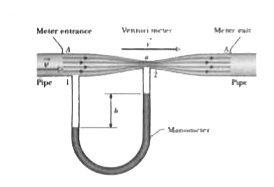
Suppose that the fluid is fresh water , that the cross-sectional areas are 64cm2 in the pipe and 32cm2 in the throat , and that the pressure is 55 kPa in the pipe and 41 kPa in the throat , and that the pressure is 55 kPa in the pipe and 41 kPa in the throat . What is the rate of water flow in cubic meters per second ?
View SolutionA lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
View Solution
Knowledge Check
A horizontal pipe of cross-section diameter 5cm carries water at a speed of 4ms−1. The pipe is connected to a smaller pipe with a cross-sectional diameter 4cm. The velocity of water through the smaller pipe is
A6.25ms−1B5.0ms−1C3.2ms−1D2.56ms−1A lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
A2.25ms−1B4.5ms−1C9ms−1D18ms−1Water is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is
Areduced to zeroBdecreased by a factor of 2Cincreased by a factor of 2Dunchanged
How many litres of water flow out of a pipe having an area of cross-section of 5cm2 in one minute, if the speed of water in the pipe is 30 cm/sec ?
View SolutionWater is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is :
View SolutionWater is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is :
View SolutionWater is flowing through a horizontal pipe of non-uniform cross- section. At the extreme narrow portion of the pipe, the water will have
View SolutionOil ( ρ=925kg/m3) is flowing through a pipeline at a constant speed when it encounters a vertical bend in the pipe raising it 4.0 m. The cross-sectional area of the pipe does not change . What is the difference in pressure (pB−pA) in the portions of the pipe before and after the rise ?
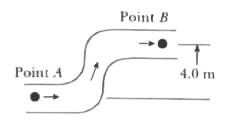
View Solution
