A transverse wave traveling along an x axis has the form given by y=ymsin(kx±ωt+ϕ).
Figure 16-10a gives the displacements of string elements as a function fo x, all at time t=0. Figure. 16-10b gives the displacements of the elements at x=0 as a function of t. Find the values of the quantities shown in Eq. 16-20. including the corret choice of sign.
(1) Figure 16-10a is effectively a snapshot of reality (something that we can see), showing us motion spread
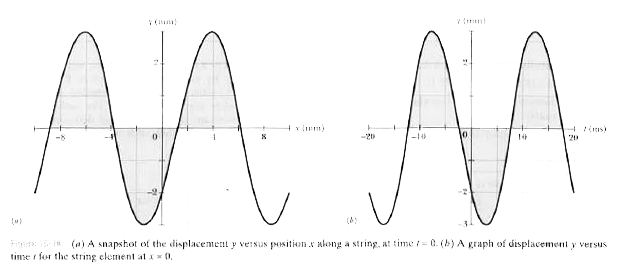
(a) A snapshot of the displacement y versus position x along a string, at time t=0. (b) A graph of displacement y versus time t for the string element at x=0.
out over the x axis. From it we can determine the wavelength λ of the wave along that axis, and then we can find the angular wave number k(=2π/λ) in Eq. 16-20. (2) Figure 16-10b is an abstraction, showing us motion spread out over time. From it we can determine the period T of the string clement in its SHM and thus also of the wave itself. From T we can then find angular frequency ω(=2π/T) in Eq. 16-20. (3) The phase constant is set by the displacement of the string at t= 0 and
Amplitude : From either Fig 16-10 a or 16-10b we see that the maximum displacement is 3.0 mm. Thus, the wave.s amplitude xm=3.0 mm.
Wavelength: In Fig. 16-10a, the wavelength λ is the distance along the x axis between repetitions in the pattern. The easiest way to measure A is to find the distance from one crossing point to the next crossing point where the string has the same slope. Visually we can roughly measure that distance with the scale on the axis. Instead, we can lay the edge of a paper sheet on the graph, mark those crossing points, slide the sheet to align the left-hand mark with the origin, and then recud oli the location of the right-hand mark Either way we find λ=10nm. From Eq. 16-7, we then have k=2πλ=2π0.010m=200πrad/m
Period : The period T is the time interval that a string element.s SHM takes to begin repeating itself. In Fig. 16 10b, T is the distance along the t axis from one crossing point to the next crossing point where the plot has the same slope. Measuring the distance visually or with the aid of a sheet of paper, we find T=20 ms. From Eq 16-10, we have ω=2πT=2π0.020s=100πrad/s
Direction of travel: To find the direction, we apply a bit of reasoning to the figures In the snapshot at 10 given in Fig 16-10a, note that it the wave is moving righiward, then just alter the snapshot, the depth of the wave at x =0 should increase (mentally slide the curve slightly rightward. then instead. The wave is moving leftward, then just after the snapshot, the depth at x=0 should decrease. Now let.s check the graph in Fig. 16-10b. It tells us that just after t=0, the depth increases. Thus, the wave is moving rightward, in the positive direction of x and we choose the minus sign in Eq 16-20.
Phase constant: The value of ϕ is set by the conditions at x=0 at the instant t=0. From either figure we see that at that location and time, y=-2.0mm. Substitting these three values and also ym=3.0mm into Eq. 16-20 gives us
−2.0mm=(3.0mm)sin(0+0+ϕ)
orϕ=sin−1(−23)=−0.73rad.
Note that this is consistent with the rule that on a plot of y versus x, a negative phase constant shifts the normal sine function rightward, which is what we see in Fig 16-10a.
Equation : Now we can fill out Eq 16-20 :
y=(3.0mm)sin(200πx−100πt−0.73rad), with x in meters and t in seconds.
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Problems
60 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
A transverse wave travelling along the positive x-axis, given by y=Asin(kx−ωt) is superposed with another wave travelling along the negative x-axis given by y=Asin(kx+ωt). The point x=0 is
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?
View Solution
Knowledge Check
A transverse wave travelling along the positive x-axis, given by y=Asin(kx−ωt) is superposed with another wave travelling along the negative x-axis given by y=Asin(kx+ωt). The point x=0 is
Aa nodeBan antinodeCneither a node nor an antinodeDa node or antinode depending on tA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
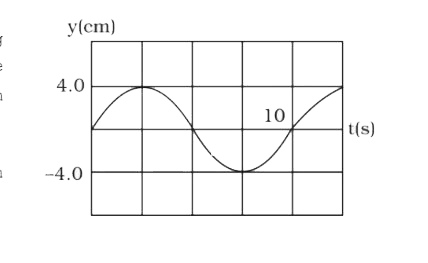
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?A−2cm/sB+2cm/sC+1.5cm/sD−2.5cm/sA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?A2cm/sB4cm/sC1cm/sD8cm/s
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
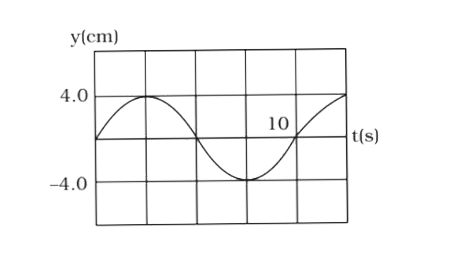
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:

View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
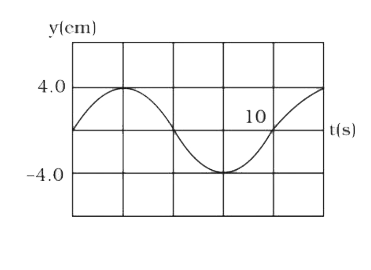
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,
View Solution
