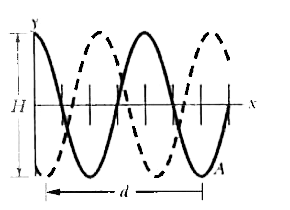
Two sinusoidal waves with the same amplitude of 4.0mm and the same wavelength traveled together along a string that is stretched along an x axis, the resultant wave due to their interference was recorded on video tape. The curves in Fig. 16-20 represent the resultant wave in two freeze frames, first as the solid curve and then, 1.0 ms later, as the dotted curve. The grid lines along the x axis are 1.0 cm apart, and the string clements oscillated vertically (perpendicular to the x axis) by 6.0 mm as the resultant wave passed through them. That wave moved a distance d =4.20 cm to the right in the 1.0 ms time interval. Write equations for the two interfering waves and for their resultant wave.
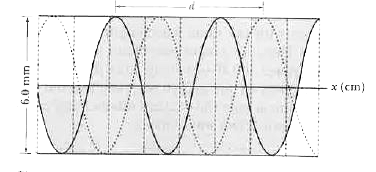
Figure 16-20 The resultant wave of two sinusoidal string wave traveling along an x axis is shown at two instants, between which the resultant wave travels distance d.
From Fig. 16-20, we see that the resultant wave is a sinusoidal wave that moves in the positive direction of the x axis. The interfering waves must both move in that direction and we can write them as
y1(x,t)=ymsin(kx−ωt)
and y2(x,t)=ymsin(kx−ωt+ϕ)
where ym=4.0mm. We can now write the resultant wave as y.(x,t)=[2y.mcos12ϕ]sin(kx−ωt+12ϕ)
The amplitude 2ymcos1/2ϕ of the resultant wave is half the total oscillation distance of 6.0 mm, so we have
2ymcos12ϕ=3.0mm
Substituting. ym=4.0mm and solving for a we get
ϕ=2cos−1(3.0mm)2(4.0mm)=136∘≈2.4rad
Thus, the phase constant in Eq. 16-59 is = 2.4 rad and the phase constant in Eq. 16-60 is 1/2 ϕ=1/(2.4+rad)≈1.2 rad,.
To find the angular wave number we use two key ideas. First, the common value of k in Eqs. 16-58 16.59 and 16-60 is related to the common wavelength equation k=2π/λ. Second, the wavelength can measured in Fig. 16-20 as the distance (parallel to the axis) between repetitions of the wave shape. Let.s use the solid curve and pick any point at which it crosses the x axis. That curve makes an identical crossing 3.0 cm to the right (or left) from the first point. Thus, λ=3.0cm, and
k=2πλ=2π0.030m=209m−1
To find the common angular frequency ω we use two more key ideas: The common value of ω in Eqs. 16-58, 16-59, and 16-60 is related to k and the common wave speed y by equation v=ω/k. That wave speed v is the ratio of the distance d traveled by the resultant wave to The time interval At required for that travel. Thus, we have ω=kv−kd△t=(209m−1)0.0420m0.0010s=8778s−1≈8800s−1
We can now write Eqs. 16-58 and 16-59 for the interfering waves as y1(x,t)=(4.0mm)sin(209x−8807)
and y2(x,t)=(4.0mm)sin(209x−8800t+2.4rad)
with x in meters and t in seconds. We can also write Eq. 16-60 for the resultant waves as y.(x,t)=(3.0mm)sin(209x−8800t+1.2rad)
again with x meters and t in seconds.
The phase difference between two waves must be 24 rad although the two wave equations can have any value of initial phase.
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Problems
60 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
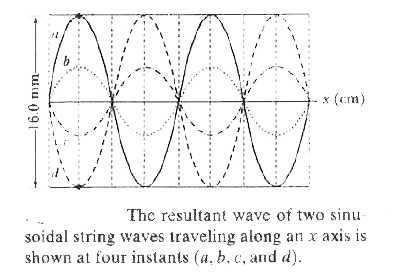
Two sinusoidal waves with the same amplitude and wavelength travel along a string that is stretched along an x axis, the resultant wave due to their superposition was recorded on video tape. The curves in Fig. 16-31 represent the resultant wave in four freeze frames in the sequence of a, b, c, and d, with 1.0 ms elapsing between curves a and d. The grid lines along the x axis are 1.0 cm apart, and the string elements oscillated perpendicular to the r axis by 16.0 mm (between the extreme displacements shown by curves a and d) as the resultant wave passed through them. Write equations for the two superposition waves and for their resultant wave.
View SolutionTwo sinusoidal waves of the same period, with amplitudes of 5.0 and 7.0 mm, travel in the same direction along a stretched string, they produce a resultant wave with an amplitude of 10.0 mm. The phase constant of the 5.0mm wave is 0. What is the phase constant of the 7.0mm wave?
View Solution
Knowledge Check
Two identical sinusoidal waves each of amplitude 5 mm with a phase difference of π/2 are traveling in the same direction in a string. The amplitude of the resultant wave (in mm) is
AzeroB5√2C5√2D2.5Two identical sinusoidal waves each of amplitude 10 mm with a phase difference of 90∘ are travelling in the same direction in a string. The amplitude of the resultant wave is
A5 mmB10√2 mmC15 mmD20 mmTwo identical sinusoidal waves each of amplitude 10 mm with a phase difference of 90∘ are travelling in the same direction in a string. The amplitude of the resultant wave is
A5 mmB10√2 mmC15 mmD20 mm
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16-53, as the antinode A travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by 15 cm, height H is 1.20 cm. Let the equation for one of the two waves be of the form y(x,t)=ymsin(kx+ω). In the equation for the other wave, what are (a)ym(b)k,(c)ω, and (d) the sign in front of ω?

View Solutiony−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
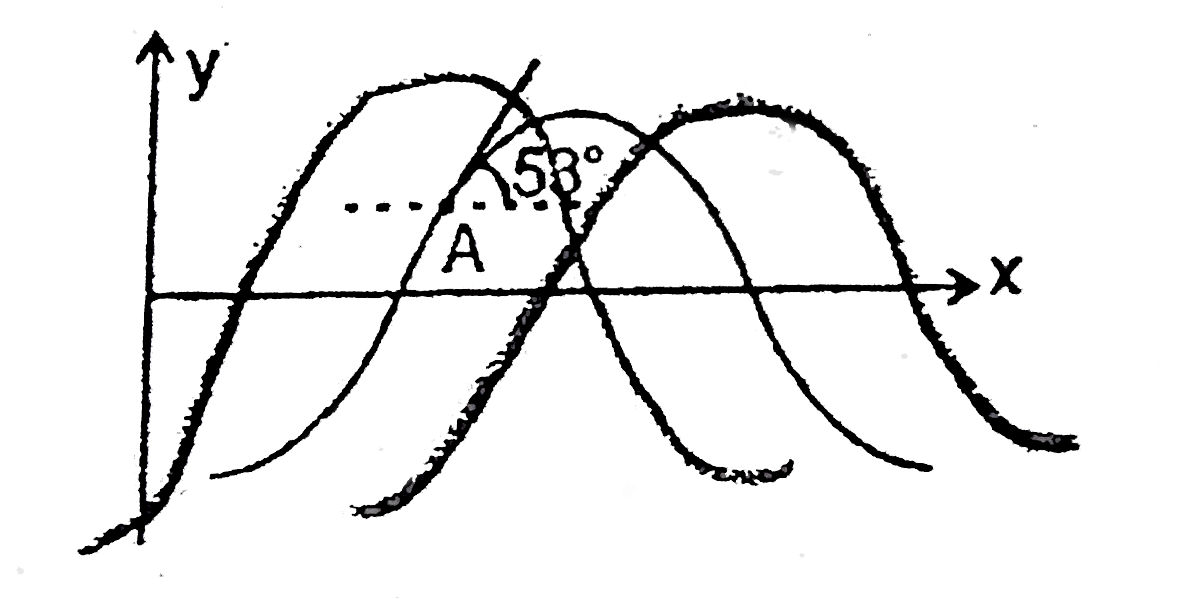
View Solutiony−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
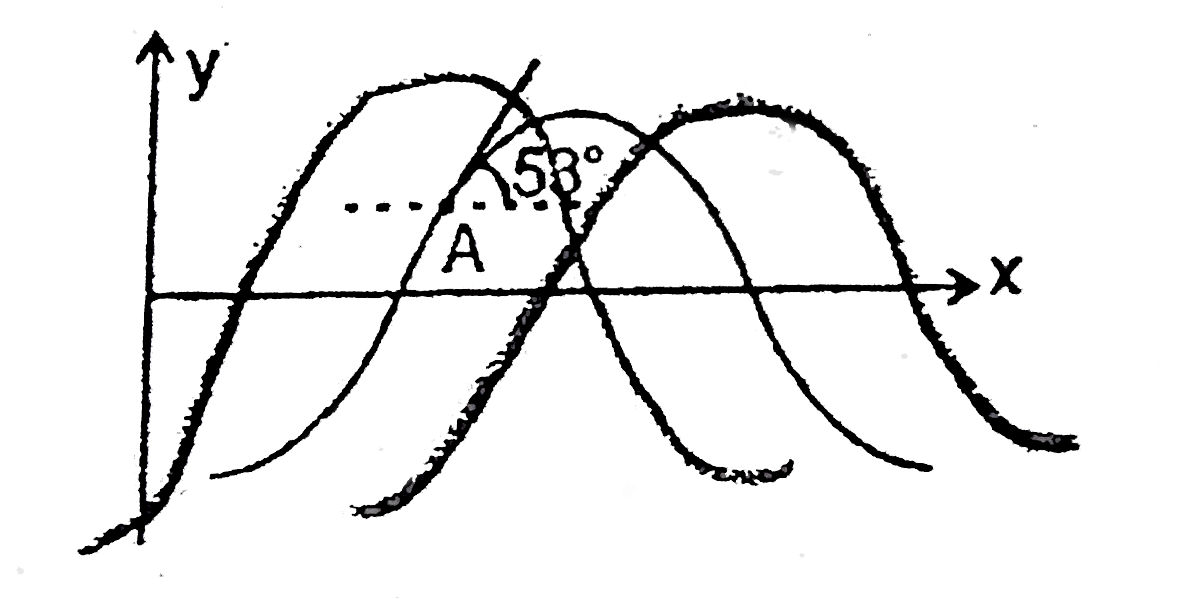
View SolutionTwo sinusoidal waves with the same amplitude of 6.00 mm and the same wavelength travel together along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16 39. as velley travels in the negative direction of the x axis by distance d= 56.0 cm in 8.0 ms. The lick matks along the axis are separated by 10cm, and height H is 8.0mm. Let the equation for one wive be of the form y(x,t) =ymsin(kx±ωt+ϕ1), where ϕ1=0 and you must choose the correct sign in front of ω. For the equation for the other wave, what are (a) ym,(b)k,(c)ω,(d)ϕ2, and (e) the sign in front of ω?
View Solutiony−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
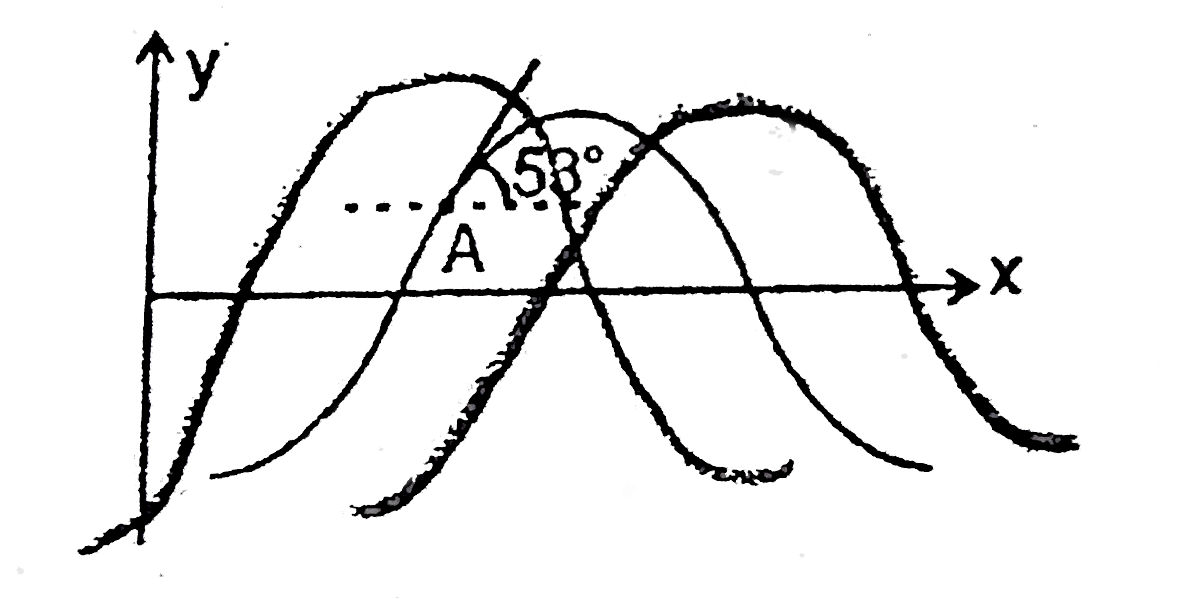
View Solution
