Consider a strong connected At both ends with rigid wall (Fig. 16-36). Find the second longest resonance wave length for which 3/8 is an antinode.
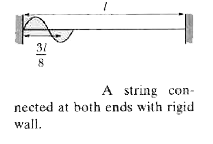
If we use normal frequencies for string with both rigid ends we can solve this problem simply by trial and error. We can consider rope of length 31/8 with one end rigid and one end free. Also, we can consider a rope of length I with both ends rigid. The frequencies which satisfy both equations simultaneously are the required frequencies. Calculations. All possible frequencies which will satisfy condition of both ends rigid:
All possible frequencies which will satisfy condition of rope of length 3/8 with one end rigid and one end free :
Only those vibrations will have resonance which satisfy , so
Therefore
3m-8n=4
The second row has the second lowest frequency, hence second largest wavelength. Therefore, on substituting value, . We can verify the answer by checking for the above value that results, in satisfying both the conditions.
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Problems
60 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
The two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second towards resonant freiquency of that pipe. Sound from pipe A set up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B in meter is :

View SolutionThe two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second towards resonant freiquency of that pipe. Sound from pipe A set up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B in meter is :

View Solution
Knowledge Check
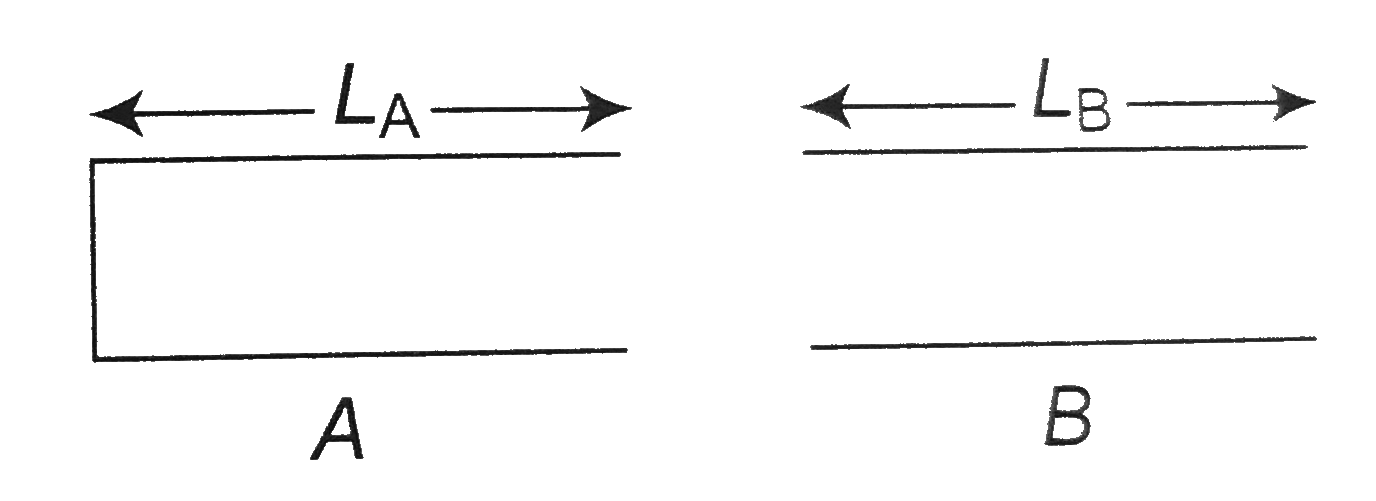
The two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second lowest resonant frequency of that pipe. Sound from pipe A sets up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B isA1mB1.5 mC2 mD3 mTwo pipes are submerged in sea water , arranged as shown in figure . Pipe (A) with length LA=1.5m and one open end , contains a small source that sets up the standing wave with the second lowest resonant frequency of that pipe . Sound from pipe A sets up resonance in pipe B , which has both ends open . The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B is :
 A1mB1.5mC2mD3m
A1mB1.5mC2mD3m

The two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second lowest resonant frequency of that pipe. Sound from pipe A sets up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B is
View SolutionTwo pipes are submerged in sea water , arranged as shown in figure . Pipe (A) with length LA=1.5m and one open end , contains a small source that sets up the standing wave with the second lowest resonant frequency of that pipe . Sound from pipe A sets up resonance in pipe B , which has both ends open . The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B is :

View SolutionA harmonic source (S) is driving a taut string. The other end of the string is tied to a wall that is not so rigid. It is observed that standing waves are formed in the string with ratio of amplitudes at the antinodes to that at the nodes equal to 8. What percentage of wave energy is transmitted to the wall?

View SolutionA rope, under tension of 200N and fixed at both ends, oscialltes in a second harmonic standing wave pattern. The displacement of the rope is given by y=(0.10)sin(πx3)sin(12πt), where x=0 at one end of the rope, x is in metres and t is in seconds. Find the length of the rope in metres.
View SolutionA rope, under tension of 200N and fixed at both ends, oscialltes in a second harmonic standing wave pattern. The displacement of the rope is given by y=(0.10)sin(πx3)sin(12πt), where x=0 at one end of the rope, x is in metres and t is in seconds. Find the length of the rope in metres.
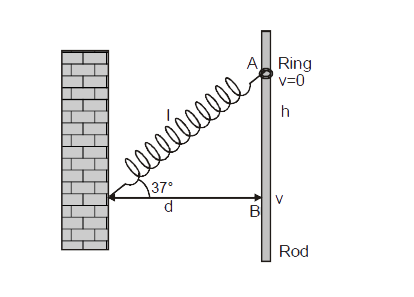
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
View Solution
