Find the particles closet to x=0.1 having same velocity as a particle at x=0.1 at t=0.
The correct Answer is:0.133
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Problems
60 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
The velocity of a particle is zero at t=0
View SolutionThe velocity of a particle is zero at t=0
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
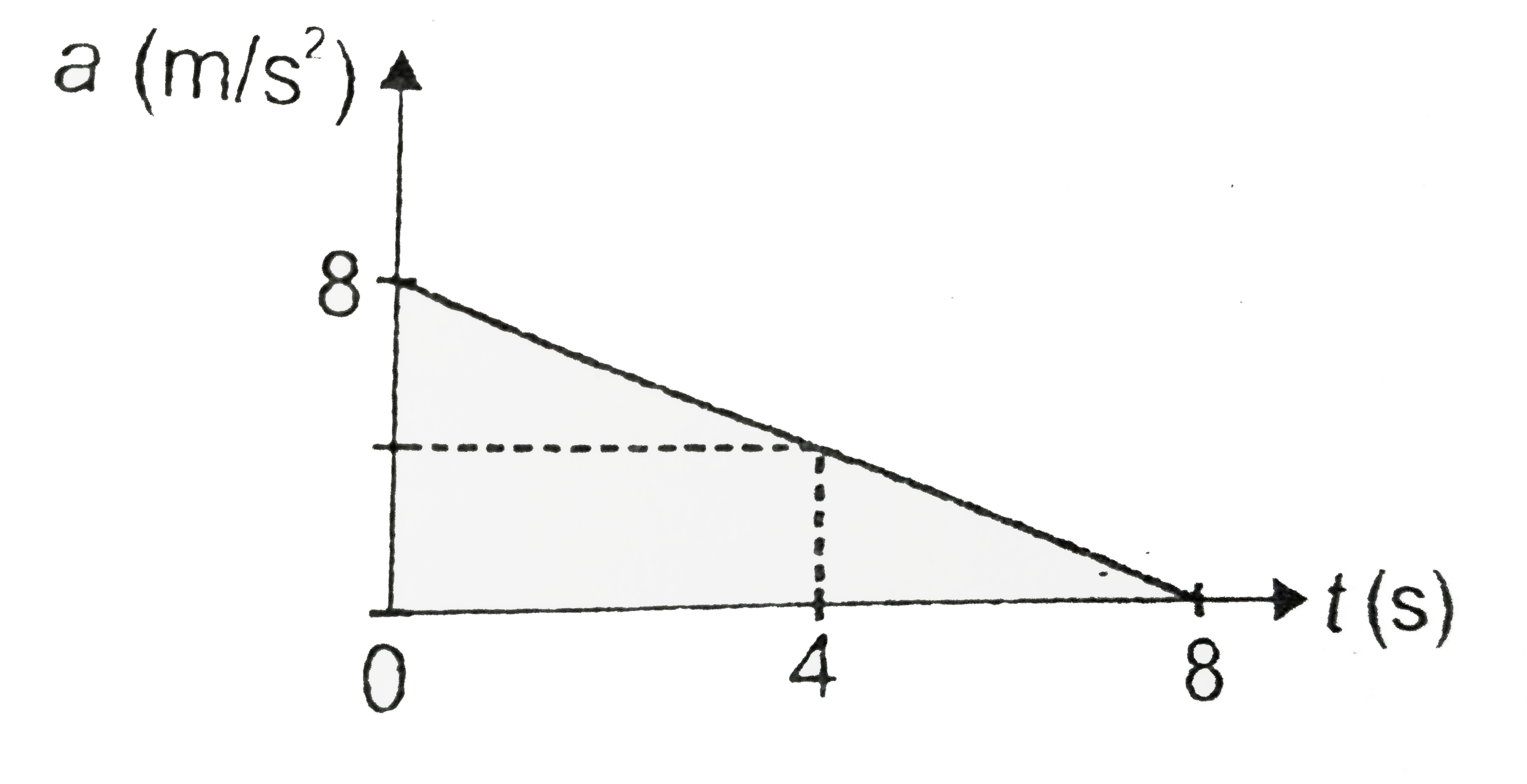
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionA hypothetical pulse is travelling along positive x direction on a taut string. The speed of the pulse is 10cms–1. The shape of the pulse at t = 0 is given as
y=x6+1for−6<x≤0=−x+1for0≤x<1=0for all other values of x
x and y are in cm.
(a) Find the vertical displacement of the particle at x = 1 cm at t = 0.2 s
(b) Find the transverse velocity of the particle at x = 1 cm at t = 0.2 s.
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionThe equation for a wave travelling in x-direction 0n a string is
y=(3.0cm)sin[(3.14cm−1x−(314s−1t]
(a) Find the maximum velocity of a particle of the string.
(b) Find the acceleration of a particle at x=6.0cm at time t=0.11s
View SolutionThe equation for a wave travelling in x-direction 0n a string is
y=(3.0cm)sin[(3.14cm−1x−(314s−1t]
(a) Find the maximum velocity of a particle of the string.
(b) Find the acceleration of a particle at x=6.0cm at time t=0.11s
View SolutionThe equation for a wave travelling in x-direction on a string is y =(3.0cm)sin[(3.14 cm^(-1) x - (314s^(-1))t] (a) Find the maximum velocity of a particle of the string. (b) Find the acceleration of a particle at x =6.0 cm at time t = 0.11 s.
View Solution
