A nylon guitar string has a linear density of 7.20 g/m and is under a tension of 180 N. The fixed supports are distance D =90.0 cm apart. The string is oscillating in the standing wave pattern shown in Fig. 16-42. Calculate the (a) speed, (b) wavelength, and (c) frequency of the traveling waves whose superposition gives this standing wave.

The correct Answer is:(a)158m/s=1.58×102m/s;(b)60.0cm;(c)264Hz
Step by step video, text & image solution for A nylon guitar string has a linear density of 7.20 g/m and is under a tension of 180 N. The fixed supports are distance D =90.0 cm apart. The string is oscillating in the standing wave pattern shown in Fig. 16-42. Calculate the (a) speed, (b) wavelength, and (c) frequency of the traveling waves whose superposition gives this standing wave. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
A nylon guiter string has a linear density of 7.20g/m and is under a tension of 150N. The fixed supports are distance D=90.0cm apart. The string is osillating in the stading wave pattern shown in figure. Calculate the (a) speed. (b) wavelength and (c) frequency of the travelling waves whose superposition gives this standing wave. ltbgt

View SolutionA string has linear density μ=525g/m and is under tension τ=45N. We send a sinusoidal wave with frequency f=120Hz and amplitude ym=8.5 mm along the string. At what average rate does the wave transport energy?
View Solution
Knowledge Check
A 2.0m long string with a linear mass density of 5.2×10−3kgm−1 and tension 52N has both of its ends fixed. It vibrates in a standing wave patten with four antinodes. Frequency of the vibraion is :-
A75 HzB150 HzC100 HzD50 HzThe velocity of waves in a string fixed at both ends is 2 m / s . The string forms standing waves with nodes 5.0 cm apart. The frequency of vibration of the string in Hz is
A40B30C20D10
A string fixed at both ends is 7.50 m long and has a mass of 0.120 kg. It is subjected to a tension of 96.0 N and set oscillating (a) What is the speed of the waves on the string? (b) What is thc longest possible wavelength for a standing wave? (c) Give the frequency of that wave.
View SolutionA string fixed at both ends is 8.40m long and has a mass of 0.120kg. It is subjected to a tension of 96.0N and set oscillating. (a) What is the speed of the waves on the string? (b) What is the longest possible wavelength for a standing wave ? (c) Give the frequency of the wave.
View SolutionA tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0.01kgm−1 kept under a tension of 49 N. The fork produces transverse waves of amplitude 0.50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string ?
View SolutionFigure 16-37 shows resonane oscillation of a string of mass m=2.500 g and lengt L= 0.800 m and that is under tension τ=325.0N. What is the wavelength λ of the transverse waves producing the standing wave patient and what is the charmant number. What is the frequency of the transverst waves and of the osciallation of the moving string elements? What is the maximum magnitude of the transverse velocity um of the element oscillating a coordinate x =0.180 m? At what point during the element's oscillation is the transverse velocity maximum?
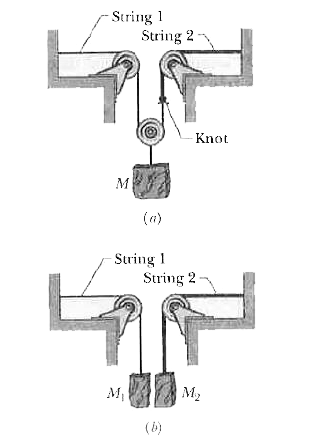
View SolutionIn fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with M1+M2=M) and the apparatus in tearranged as shown in fig. 16-47b. Find (c) M1and(d)M2 such that the wave speeds in the two strings are equal.
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View Solution
