आकृति में ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED,ACFG और ABMN क्रमश : भुजाओं BC,CA और AB पर बने वर्ग हैं। रेखाखंड AX⊥DE भुजा BC को बिंदु Y पर मिलता हैं । दर्शाइए कि :
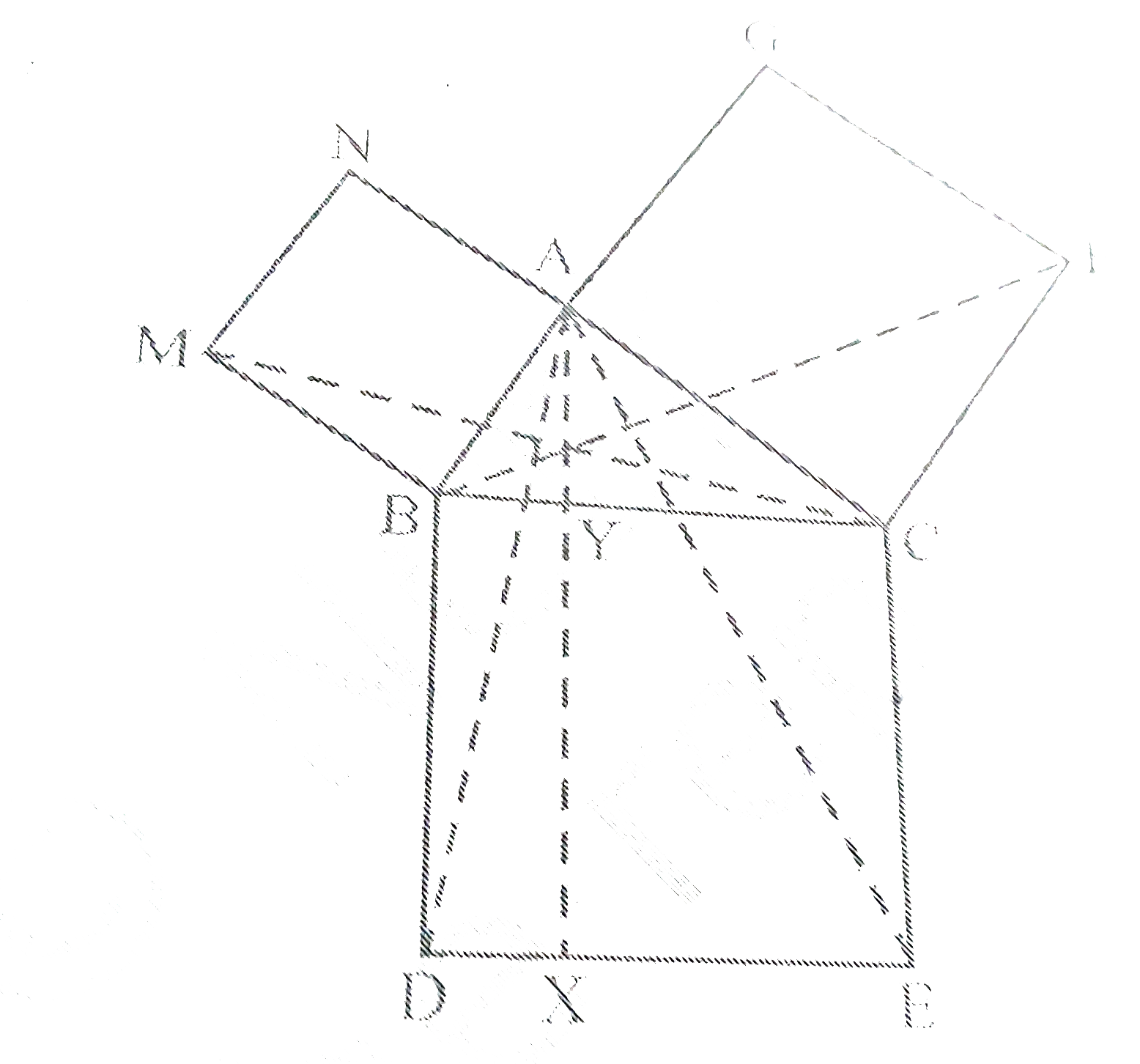
(i)ΔMBC≅ΔABD(ii)ar(BYXD)=2ar(MBC)(iii)ar(BYXD)=ar(ABMN)(iv)ΔFCB≅ΔACE(v)ar(CYXE)=2ar(FCB)(iv)ar(CYXE)=ar(ACFG)(vii)(BCED)=ar(ABMN)+ar(ACFG)
Step by step video & image solution for आकृति में ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमश : भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड AX bot DE भुजा BC को बिंदु Y पर मिलता हैं । दर्शाइए कि : {:((i)Delta MBC~=Delta ABD ,(ii)ar(BYXD)=2ar(MBC)),((iii)ar(BYXD)=ar(ABMN),(iv)Delta FCB ~= Delta ACE ),((v)ar(CYXE)=2ar(FCB),(iv)ar(CYXE)=ar(ACFG)),((vii)(BCED)=ar(ABMN)+ar(ACFG),):} by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NCERT HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.316videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1.63videos
संख्या पद्धति
- BOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.46videos
सांख्यिकी
Similar Questions
आकृति में, ΔABC की एक मध्यिका AD पर स्थित E कोई बिंदु है दर्शाइए कि ar(ABE)=ar(ACE) है।
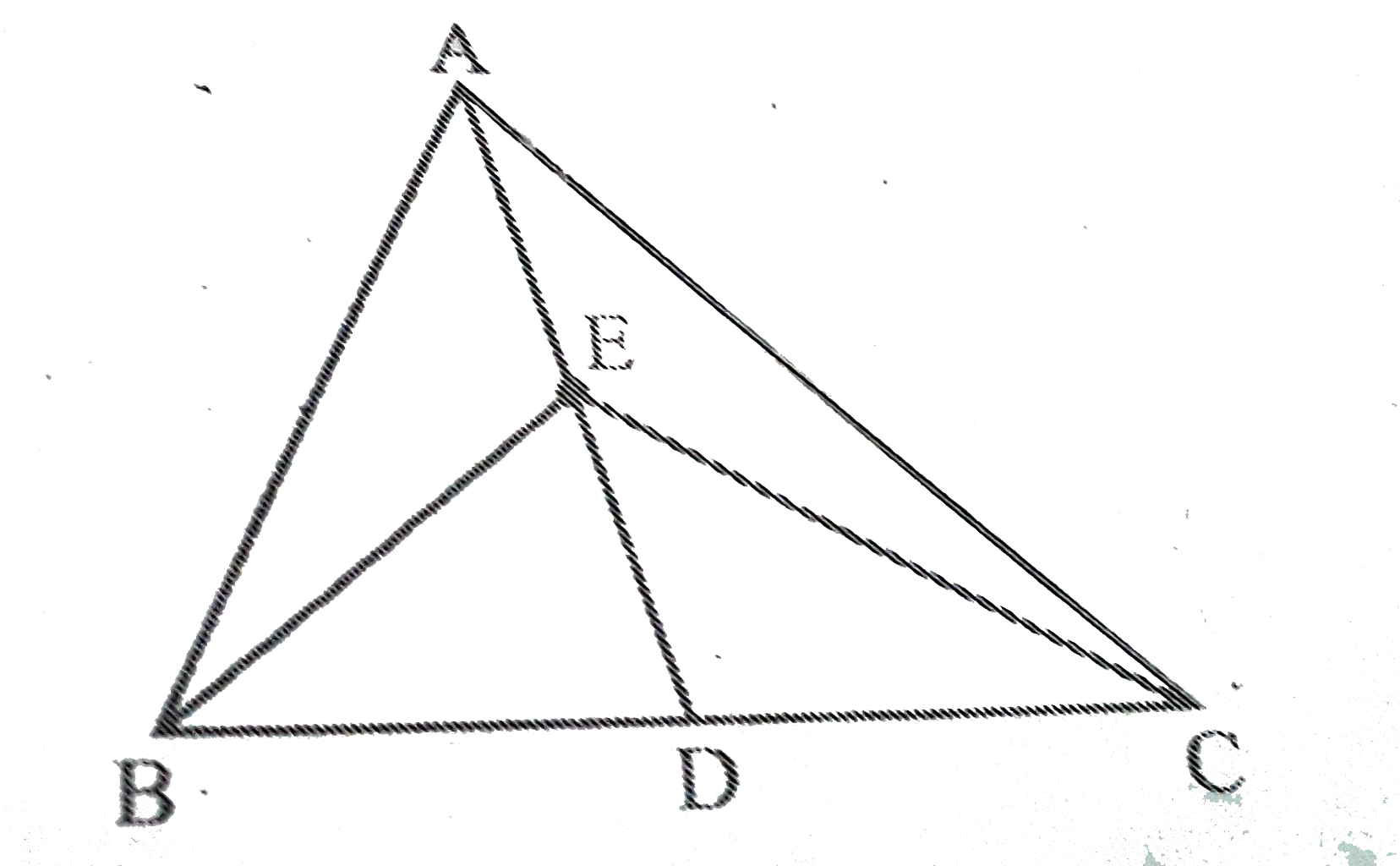 01:47View Solution
01:47View Solutionज्ञात कीजिए : (i) 6412 (ii)3215 (iii)12513
02:35View Solutionएक टीम ने फुटबॉल के 10 मैचों में निम्नलिखित गोल किएः
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए:03:40View Solutiontriangle ABC में, जिसका B कोण समकोण है, AB = 12 cm और BC = 5 cm है। sin C का मान है :
03:22View Solution△ ABC में, जिसका कोण B समकोण है, AB = 5 cm और, BC = 12 cm है। cos C का मान है :
03:09View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
04:20View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
06:37View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
04:29View SolutionIn △ABC ,D and E are the points on sides AB and AC, respectively, such that DE || BC. If DE : BC is 3 : 5, then (Area of △ADE): (Area of quadrilateral DECB) is:
त्रिभुज ABC में, D तथा E भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि DE || BC है | यदि DE : BC= 3 : 5, है, तो (△ADE का क्षेत्रफल ): ( DECB का क्षेत्रफल ) ज्ञात करें |04:12View SolutionIn a △ABC, D and E are two points on the sides AB and BC , respectively such that AD : DB = 2: 3 and DE || AC. If the area of △ADE is equal to 18 square cm, then what is the area ( In square cm) of △ABC ?
किसी त्रिभुज ABC में, D और E क्रमश: भुजा AB और BC पर स्थित बिंदु हैं जो इस प्रकार हैं कि AD : DB = 2: 3 है तथा 9DE || AC है | यदि त्रिभुज ADE का क्षेत्रफल 18 वर्ग सेमी के बराबर है, तो त्रिभुज ABC का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें05:03View SolutionIn △ABC ,D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD /BD = 3/4 ,Then ratio of the area of trapezium DECB to the area of △ABC is:
त्रिभुज ABC में, D तथा E भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि DE || BC और AD/BD = 3/4 है | समलम्ब DECB के क्षेत्रफल और त्रिभुज ABC के क्षेत्रफल में अनुपात ज्ञात करें ।06:40View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |05:38View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =5/6 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =5/6 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल के बीच अनुपात ज्ञात करें |02:17View SolutionIf in triangle ABC , D and E are the points on sides AC and BC, respectively such that DE || AB. F is the point on CE such that DF ||AE. If CE= 6cm and CF = 2.5 cm, then BC is equal to: त्रिभुज ABC में, D और E क्रमशः भुजाओं AC तथा BC के मध्य बिंदु हैं जो इस प्रकार ह कि DE || AB है F, CE पर स्थित ऐसा बिंदु है कि DF|| AE है | यदि CE= 6 सेमी और CF =2.5 सेमी है, तो BC किसके बराबर है ?
03:27View SolutionIn triangle ABC , angle A = 90^@ , AD is the bisector of angle A meeting BC at D and DE bot AC at E. If AB =10cm and AC = 15 cm, then the length of DE, in cm is: triangle ABC में angle A=90^@ , AD, angle A का द्विभाजक है, जो BC से D पर मिलता है, और DE bot AC से E पर मिलता है। यदि AB = 10 cm और AC= 15 cm है, तो DE की लंबाई(cm) है,
11:38View SolutionIn angle ABC , D and E are the midpoint of sides BC and AC, respectively AD and BE intersect at G at right angle. If AD= 18cm and BE = 12cm then the length of DC (in cm) is : त्रिभुज ABC में, D और E भुजाओं BC और AC के मध्य बिंदु हैं, क्रमश AD और BE समकोण पर G पर प्रतिच्छेद करते ह। यदि AD = 18 सेमी और BE = 12 सेमी तो DC (सेमी में) की लंबाई है:
06:53View Solution

