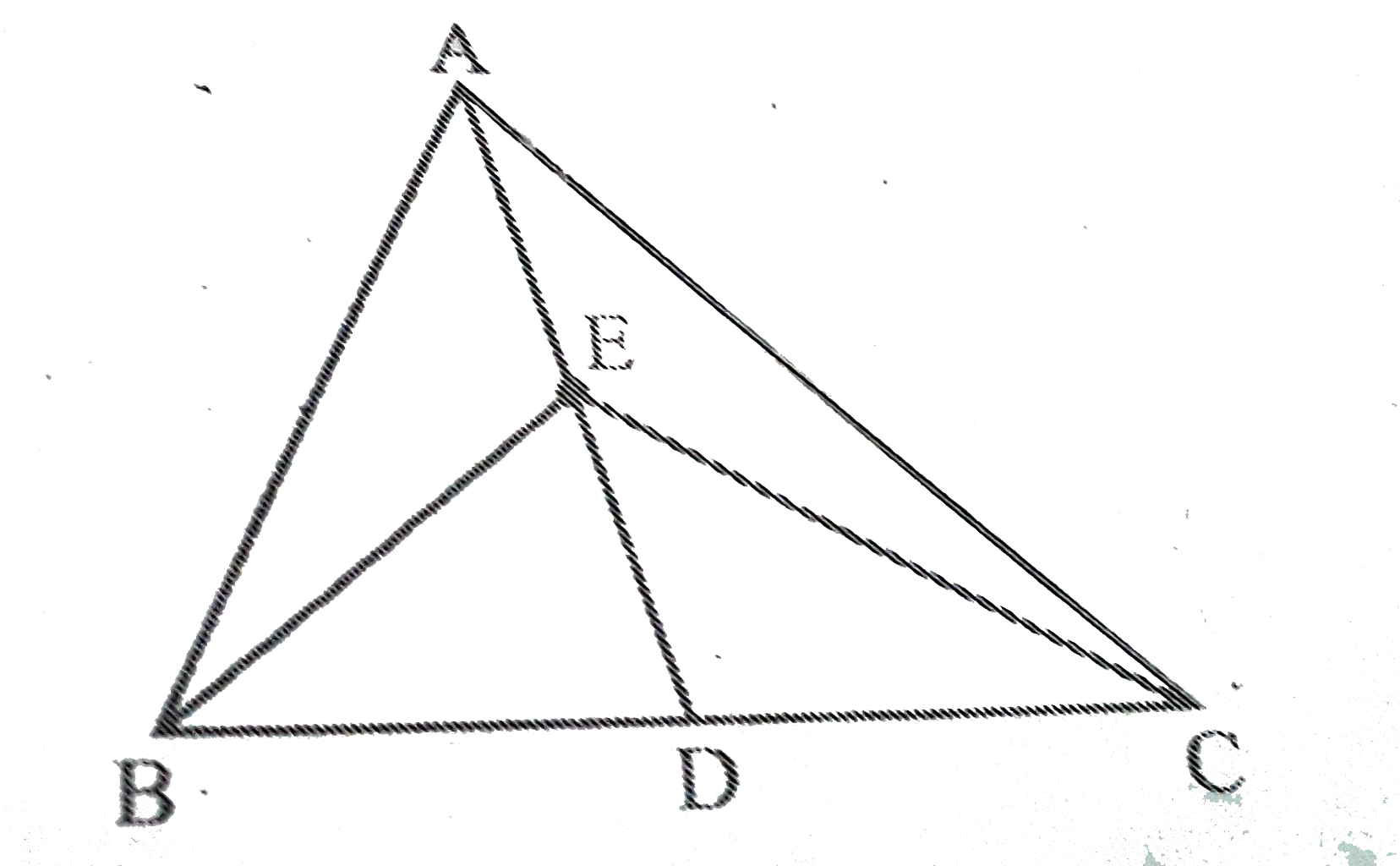
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
(i) ar(BDE)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE)
(iii) ar(ABC)=2ar(BEC)
(iv) ar(BFE)=ar(AFD)
(v) ar(BFE)=2ar(FED)
(vi) ar(FED)=18ar(AFC)
Step by step video & image solution for आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि (i) ar (BDE) = 1/4ar (ABC) (ii) ar (BDE) = 1/2ar (BAE) (iii) ar (ABC) = 2 ar (BEC) (iv) ar (BFE) =ar (AFD) (v) ar ( BFE) = 2 ar (FED) (vi) ar (FED) = 1/8ar (AFC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NCERT HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.316videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1.63videos
संख्या पद्धति
- BOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.46videos
सांख्यिकी
Similar Questions
आकृति में, ΔABC की एक मध्यिका AD पर स्थित E कोई बिंदु है दर्शाइए कि ar(ABE)=ar(ACE) है।
 View Solution
View Solutionज्ञात कीजिए : (i) 6412 (ii)3215 (iii)12513
01:21View Solutionएक टीम ने फुटबॉल के 10 मैचों में निम्नलिखित गोल किएः
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए:03:37View Solutionदिए गए आकृति में ABC और BDF दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य बिंदु है |यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाई की
ar(BDF)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE) ltBrgt (iii) ar(ABC)=2ar(BEC)
(iv) ar(BEF)=ar(AFD) ltBrgt (v) ar(BEF)=2ar(FED)
(vi)ar(FED)=18ar(AFC)07:33View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
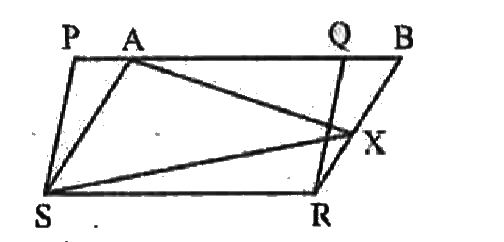
00:49View SolutionIn, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
as (AXS) = 12 ar (PQRS)
 View Solution
View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).02:29View SolutionFactorise:
ar+br+at+bt01:45View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)06:30View Solutionआकृति में PQRS और ABRS समांतर चतुर्भज है तथा x भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
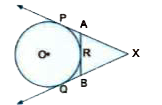
ar(AXS)=12ar(PQRS)01:52View SolutionIn the Fig Prove that XA+AR=XB+BR.
 03:07View Solution
03:07View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
01:32View SolutionFind the odd man out : F, Cl, Ar, Br
01:28View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
06:45View Solutionगुणनखण्ड निकालें:
ar+br+at+bt02:37View Solutionar + br + at + bt = __
03:21View Solution

