The disk in Fig. 10-5a is rotating about its central axis like a merry-go-round. The angular position $θ (t)$ of a reference line on the disk is given by
$θ = - 1.00 - 0.600 t + 0.250 t^{2}$ ,
with t in seconds, $θ$ radians, and the zero angular position as indicated in the figure.
(a) Graph the angular position of the disk verus time from t = -3.0 s to t = 5.4 s. Sketch the disk and its angular position reference line at t = -2.0 s, 0 s, and 4.0 s, and when the curve crosses the t axis.
(b) At what time $t_{min} does θ (t)$ reach the minimum value shown in Fig. 10-5b? What is that minimum value?
(c ) Graph the angular velocity $ω$ of the disk versus time from t = -3.0 s to t = 6.0 s. Sketch the disk and indicate the direction of turning and the sign of $ω$ at t = -2.0 s, 4.0 s, and $t_{min}$ .
(d) Use the results in parts (a) through ( c) to describe the motion of the disk from t = -3.0 s to t = 6.0 s.

Text Solution

Verified by Experts

(a) The angular position of the disk is the angular position $θ (t)$ of its reference line, which is given by a function of time t. So we graph, the result is shown in Fig.
Calculations: To sketch the disk and its reference line at a particular time, we need to determine $θ$ for that time. To do so, we substitute the time. For t = -2.0 s, we get
$θ = - 1.00 - (0.600) (- 2.0) + (0.250) {(- 2.0)}^{2}$
= $1.2 r a d = 1.2 r a d \frac{360^{\circ}}{2 π r a d} = 69^{\circ}$ .
This means that at t = -2.0 s the reference line on the disk is rotated counterclockwise from the zero position by angle 1.2 rad = $69^{\circ}$ (counterclockwise because $θ$ is positive). Sketch 1 in Fig. shows this position the reference line.
Similarly, for t = 0, we find $θ = - 1.00 r a d = - 57^{\circ}$ , which means that the reference line is rotated clockwise from the zero angular position by 1.0 rad, or $57^{\circ}$ , as shown in sketch 3. For t = 4.0 s, we find $θ = 0.60 r a d = 34^{\circ}$ . Drawing sketches for when the curve crosses the t axis is easy, because then $θ$ = 0 and the reference line is momentarily aligned with the zero angular position.

(b) To find the extreme value of a function, we take the first derivative of the function and set the result to zero.
Calculations: The first derivative of $θ (t)$ is
$\frac{d θ}{d t} = - 0.600 + 0.500 t$
Setting this to zero and solving for t give us the time at which $θ (t)$ is minimum:
$t_{min} = 1.20 s$ .
To get the minimum value of $θ$ , we next substitute $t_{min}$ into Eq. finding
$θ = - 1.36 r a d \approx - {77.9}^{\circ}$ .
This minimum of $θ (t)$ corresponds to the maximum clockwise rotation of the disk from the zero angular position, somewhat more than is shown in sketch 3.
( c) From the angular velocity $ω$ is equal to $d θ / d t$ as given in Eq. So, we have
$ω = - 0.600 + 0.500 t$ .
The graph of this function $ω (t)$ is shown in Fig. Because the function is linear, the plot is a straight line. The slope is 0.500 $r a d / s^{2}$ and the intercept with the vertical axis is -0.600 rad/s.
Calculations: To sketch the disk at t = -2.0 s, we substitute that value into Eq., obtaining
$ω = - 1.6 r a d / s$ .
The minus sign here tells us that at t = -2.0 s, the disk is turning clockwise.
Substituting t = 4.0 s into Eq. given us

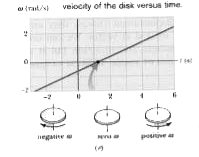
The implied plus sign tells us that now the disk is turning counterclockwise.
For $t_{min}$ , we already known that $d θ / d t = 0$ . So, we must also have $ω = 0$ . That is, the disk momentarily stops when the reference line reaches the minimum value of $θ$ in Fig. as suggested by the center sketch in Fig. On the graph of $ω$ versus t in Fig. this momentary stop is the zero point where the plot changes from the negative clockwise motion to the positive counterclockwise motion.
(d) Description: When we first observe the disk at t = -3.0s, it has a positive angular position and is turning clockwise but slowing. It stops at angular position $θ = - 1.36$ rad and then begins to turn counterclockwise, with its angular position eventually becoming positive again.

Updated on:21/07/2023