A tall, cylindrical chimney starts falling over as shown in Fig. Treat the chimney as a thin rigid rod of length L = 55.0 m. At the instant it makes as angle of θ=60.0∘m with the vertical, what is its angular speed ωf?
To find the angular speed ωf of a falling cylindrical chimney modeled as a thin rigid rod at an angle of θ=60∘ with the vertical, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Identify the initial and final states
- Initial State (Point A): The chimney is vertical, and its center of mass is at a height L2 from the ground.
- Final State (Point B): The chimney is at an angle of 60∘ with the vertical. The center of mass is now at a height of L2cos(60∘).
Step 2: Write the conservation of energy equation
The total mechanical energy at the initial state must equal the total mechanical energy at the final state:
Potential Energy at A=Kinetic Energy at B+Potential Energy at B
mghA=12Iω2f+mghB
Step 3: Calculate the heights
- Height at Point A: hA=L2
- Height at Point B:
hB=L2cos(60∘)=L2⋅12=L4
Step 4: Substitute the heights into the energy equation
Substituting the heights into the energy equation:
mg⋅L2=12Iω2f+mg⋅L4
Step 5: Moment of inertia of the rod
The moment of inertia I of a thin rod rotating about one end is given by:
I=13mL2
Step 6: Substitute I into the energy equation
Substituting I into the energy equation:
mg⋅L2=12(13mL2)ω2f+mg⋅L4
Step 7: Simplify the equation
Cancelling m from both sides (assuming m≠0):
g⋅L2=16L2ω2f+g⋅L4
Step 8: Rearranging the equation
Rearranging gives:
g⋅L2−g⋅L4=16L2ω2f
g⋅L4=16L2ω2f
Step 9: Solve for ω2f
Multiplying both sides by 6:
6g⋅L4=L2ω2f
3gL2=L2ω2f
Step 10: Solve for ωf
Dividing both sides by L2:
ω2f=3g2L
Taking the square root:
ωf=√3g2L
Step 11: Substitute values
Substituting g=9.8m/s2 and L=55.0m:
ωf=√3⋅9.82⋅55.0=√29.4110=√0.267≈0.517rad/s
Final Answer
Thus, the angular speed ωf of the chimney at an angle of 60∘ with the vertical is approximately 0.517rad/s.
- Initial State (Point A): The chimney is vertical, and its center of mass is at a height L2 from the ground.
- Final State (Point B): The chimney is at an angle of 60∘ with the vertical. The center of mass is now at a height of L2cos(60∘).
The total mechanical energy at the initial state must equal the total mechanical energy at the final state:
Potential Energy at A=Kinetic Energy at B+Potential Energy at B
mghA=12Iω2f+mghB
- Height at Point A: hA=L2
- Height at Point B:
hB=L2cos(60∘)=L2⋅12=L4
Substituting the heights into the energy equation:
mg⋅L2=12Iω2f+mg⋅L4
The moment of inertia I of a thin rod rotating about one end is given by:
I=13mL2
Substituting I into the energy equation:
mg⋅L2=12(13mL2)ω2f+mg⋅L4
Cancelling m from both sides (assuming m≠0):
g⋅L2=16L2ω2f+g⋅L4
Rearranging gives:
g⋅L2−g⋅L4=16L2ω2f
g⋅L4=16L2ω2f
Multiplying both sides by 6:
6g⋅L4=L2ω2f
3gL2=L2ω2f
Dividing both sides by L2:
ω2f=3g2L
Taking the square root:
ωf=√3g2L
Substituting g=9.8m/s2 and L=55.0m:
ωf=√3⋅9.82⋅55.0=√29.4110=√0.267≈0.517rad/s
Thus, the angular speed ωf of the chimney at an angle of 60∘ with the vertical is approximately 0.517rad/s.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT18videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS100videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
A tall, cylindrical chimney falls over when its base is ruptured. Treat the chimney as a thin rod of length 55.0 m. At the instant it makes an angle of 35.0∘ with the vertical as it falls, what are (a) the radial acceleration of the top, and (b) the tangential acceleration of the top. ( c) At what angle θ is the tangential acceleration equal to g?
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mas m and length l is made to stand at an angle of 60∘ with the vertical. What is the potential energy of the rod in this position?
AmglBmgl2Cmgl3Dmgl4 - Question 2 - Select One
A pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
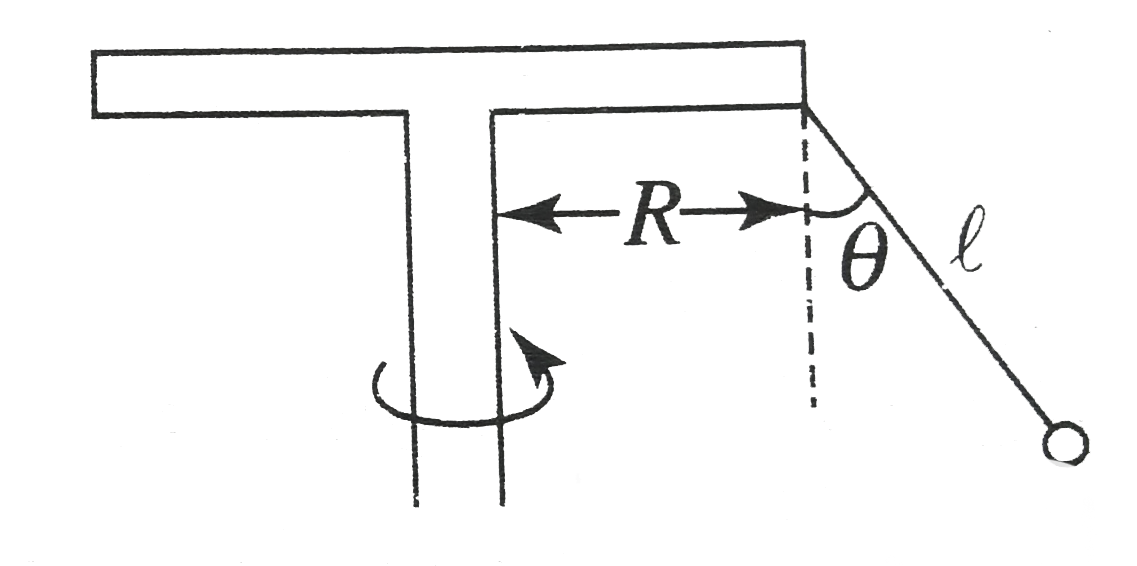 Aω=√>anθR+lsinθBω=√>anθR+<anθCω=√gcotθR+lsinθDω=√>anθR+lcosθ
Aω=√>anθR+lsinθBω=√>anθR+<anθCω=√gcotθR+lsinθDω=√>anθR+lcosθ - Question 3 - Select One
The induced e.m.f. in a rod of length l translating at a speed v making an angle θ with length l and perpendicular to magnetic field B is
AB/vBB/v cosθCB/v sinθDB/v tanθ
A rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View SolutionA child is swinging a ball of mass M around on a light spring which has spring constant k. The ball describes a horizontal circle. The stretched spring has a length a horizontal circle. The stretched spring has a length l and makes an angle θ with the vertical as shown in fig. the acceleration due to gravity is g neglect air resistance.
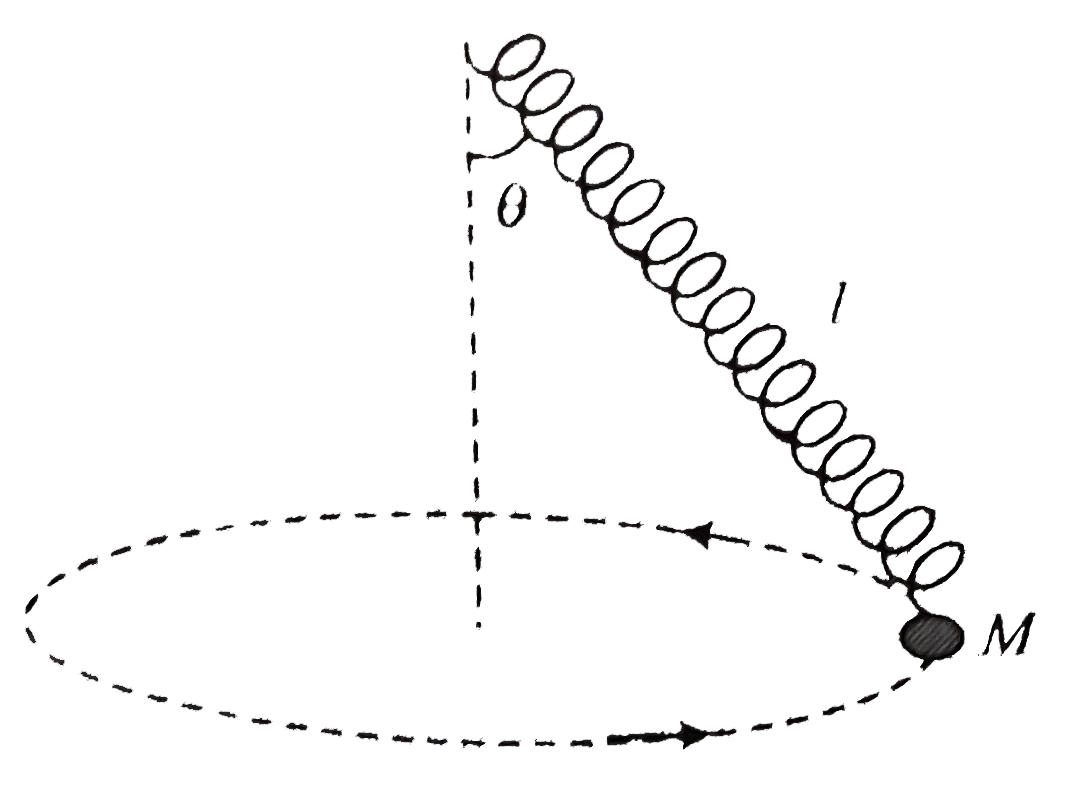
a. In terms of only the given quantities , what is the magnitude of force F that the spring exerts on man M?
b.In terms of F,kand lwhat is the natural length l0 of the spring i.e. the length of the spring when it is not steched?
c. In terms of F,l,M and B what is the speed v of the ball?View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
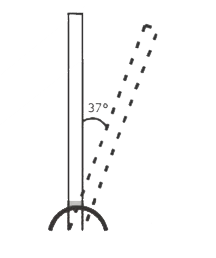 View Solution
View SolutionA rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
View SolutionThe rod shown in fig starts slipping. Find the speed of lower end if the speed of upper end is √2m/s when it makes an angle 45∘ with the x axis
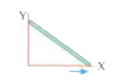 View Solution
View Solution

