A tall, cylindrical chimney falls over when its base is ruptured. Treat the chimney as a thin rod of length 55.0 m. At the instant it makes an angle of 35.0∘ with the vertical as it falls, what are (a) the radial acceleration of the top, and (b) the tangential acceleration of the top. ( c) At what angle θ is the tangential acceleration equal to g?
To solve the problem step by step, we will break it down into parts (a), (b), and (c) as outlined in the question.
Given:
- Length of the chimney (L) = 55.0 m
- Angle with the vertical (θ) = 35.0°
(a) Radial Acceleration of the Top
1. Identify the center of mass: For a thin rod, the center of mass is at L/2.
2. Calculate the height (h) fallen by the center of mass:
h=L2−L2cos(35∘)=L2(1−cos(35∘))
Substituting L=55.0 m:
h=55.02(1−cos(35∘))≈27.5(1−0.8192)≈27.5×0.1808≈4.97 m
3. Use conservation of energy: The increase in rotational kinetic energy equals the decrease in potential energy.
12Iω2=mgh
For a rod rotating about one end, the moment of inertia I=13mL2:
12(13mL2)ω2=mgh
Cancel m from both sides:
16L2ω2=gh
Substitute h:
16(55.0)2ω2=9.8×4.97
Calculate gh:
gh≈9.8×4.97≈48.8
Now solve for ω2:
ω2=6×48.855.02≈292.83025≈0.0967 rad2/s2
4. Calculate radial acceleration:
ac=ω2L=0.0967×55.0≈5.31 m/s2
(b) Tangential Acceleration of the Top
1. Calculate the torque (τ):
τ=mg(L2)sin(35∘)
Substitute m and simplify:
τ=mgL2sin(35∘)=mLg2sin(35∘)
2. Apply the rotational dynamics equation:
τ=Iα
Substitute I:
mLg2sin(35∘)=13mL2α
Cancel m and L:
gsin(35∘)2=13Lα
Solve for α:
α=3gsin(35∘)2L
3. Calculate tangential acceleration:
at=αL=3gsin(35∘)2
Substitute g:
at=3×9.8×0.57362≈16.832≈8.415 m/s2
(c) Angle θ when Tangential Acceleration equals g
1. Set tangential acceleration equal to g:
3gsin(θ)2=g
Cancel g:
3sin(θ)2=1⇒sin(θ)=23
2. Calculate θ:
θ=sin−1(23)≈41.81∘
Final Answers:
(a) Radial acceleration of the top = 5.31 m/s²
(b) Tangential acceleration of the top = 8.415 m/s²
(c) Angle θ when tangential acceleration equals g = 41.81°
- Length of the chimney (L) = 55.0 m
- Angle with the vertical (θ) = 35.0°
2. Calculate the height (h) fallen by the center of mass:
h=L2−L2cos(35∘)=L2(1−cos(35∘))
Substituting L=55.0 m:
h=55.02(1−cos(35∘))≈27.5(1−0.8192)≈27.5×0.1808≈4.97 m
12Iω2=mgh
For a rod rotating about one end, the moment of inertia I=13mL2:
12(13mL2)ω2=mgh
Cancel m from both sides:
16L2ω2=gh
Substitute h:
16(55.0)2ω2=9.8×4.97
Calculate gh:
gh≈9.8×4.97≈48.8
Now solve for ω2:
ω2=6×48.855.02≈292.83025≈0.0967 rad2/s2
ac=ω2L=0.0967×55.0≈5.31 m/s2
τ=mg(L2)sin(35∘)
Substitute m and simplify:
τ=mgL2sin(35∘)=mLg2sin(35∘)
τ=Iα
Substitute I:
mLg2sin(35∘)=13mL2α
Cancel m and L:
gsin(35∘)2=13Lα
Solve for α:
α=3gsin(35∘)2L
at=αL=3gsin(35∘)2
Substitute g:
at=3×9.8×0.57362≈16.832≈8.415 m/s2
3gsin(θ)2=g
Cancel g:
3sin(θ)2=1⇒sin(θ)=23
θ=sin−1(23)≈41.81∘
(a) Radial acceleration of the top = 5.31 m/s²
(b) Tangential acceleration of the top = 8.415 m/s²
(c) Angle θ when tangential acceleration equals g = 41.81°
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)43videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT18videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
A tall, cylindrical chimney starts falling over as shown in Fig. Treat the chimney as a thin rigid rod of length L = 55.0 m. At the instant it makes as angle of θ=60.0∘m with the vertical, what is its angular speed ωf?
View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at an angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?View Solution
Knowledge Check
- Question 1 - Select One
A point size mass 100gm is rotated in a vertical circle using a cord of length 20cm. When the string makes an angle 60∘ with the vertical, the speed of the mass is 1.5m/s. The tangential acceleration of the mass in that position is (in ms−2).
A4.9B4.9√2C4.9√3D9.8 - Question 2 - Select One
A simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
Amv2/LBmgcosθ+mv2/LCmgcosθ−mv2/LDmgcosθ - Question 3 - Select One
A pencil is placed vertically on a table top with its point end up and its sticky eraser end down As it falls over from this unstable. Position. Its point of contact with the tangential acceleration of its tip.
 Adecreasing continuouslyB.exceeds g at some instantCbecomes g just before hitting the tableDIS constant
Adecreasing continuouslyB.exceeds g at some instantCbecomes g just before hitting the tableDIS constant
Water is filled in a container having square base (2m×2m).Height of water in the container is h=2m . Now the container is tilted so that its base makes an angle of 30∘ with the horizontal.The tilted container is accelerated to right with a horizontal acceleration of a=2ms2 .Now the water surface makes an angle a with horizontal. If the value of α is tan−1(1x) ,then what is the value of x(g=10ms2)?
View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View SolutionFigure shows a smasll sphereical bal of mass m rolling down the loop track. Thebasll is released on the linear portion at a verticla height H from the lowest point. The circular part show has a radius R.
a. find the kinetic energy of the ball when it is at a point where the radius makes an angle θ with the horizontal.
Find the radial and the tangential accelerations of the cente when the ball is at A. c. find the bnormal force and the frictionasl force acting on the ball if H=60 cm, R=10cm θ=0 and m=70 fg.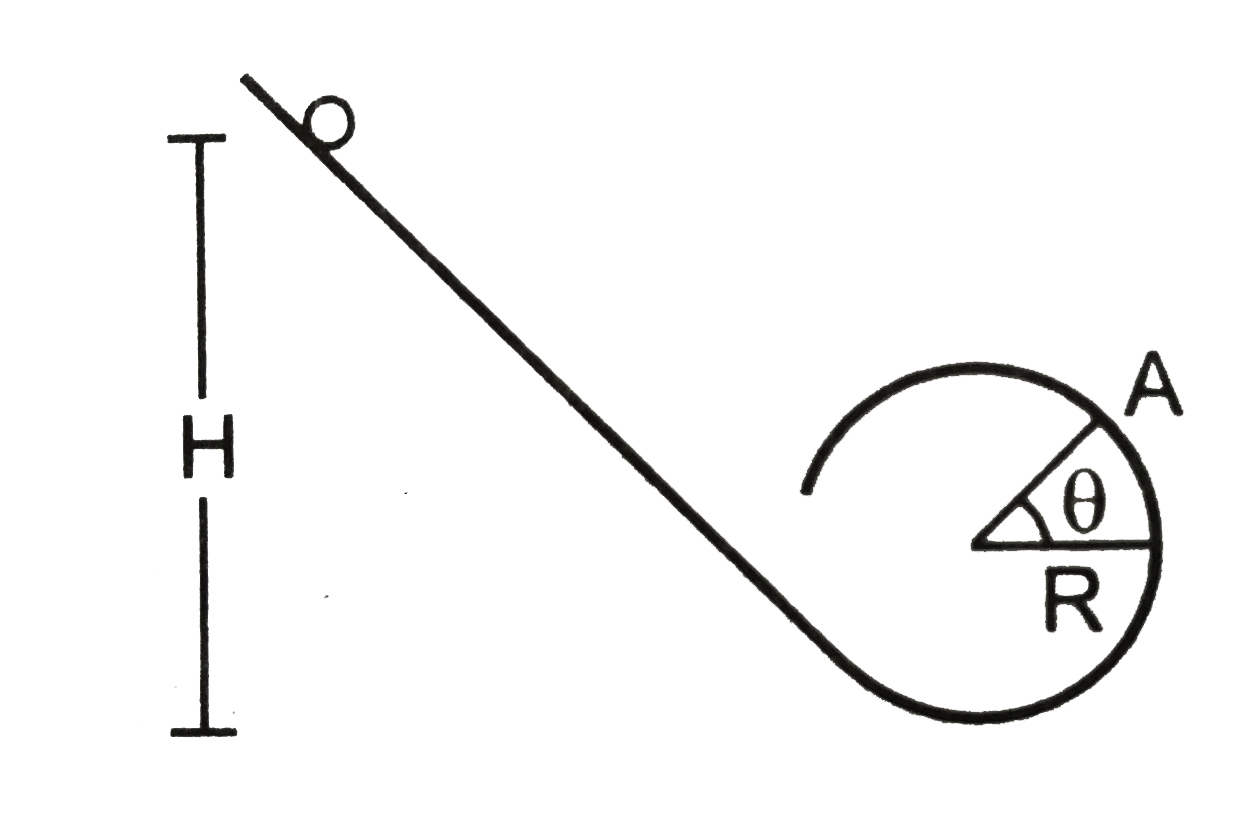 View Solution
View SolutionA body of mass 4 kg is moved in a vertical circle with sufficient speed .Its tangential acceleration , when the string makes an angle of 30∘ with the verticle downward is (g=10mms2)
View SolutionA slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
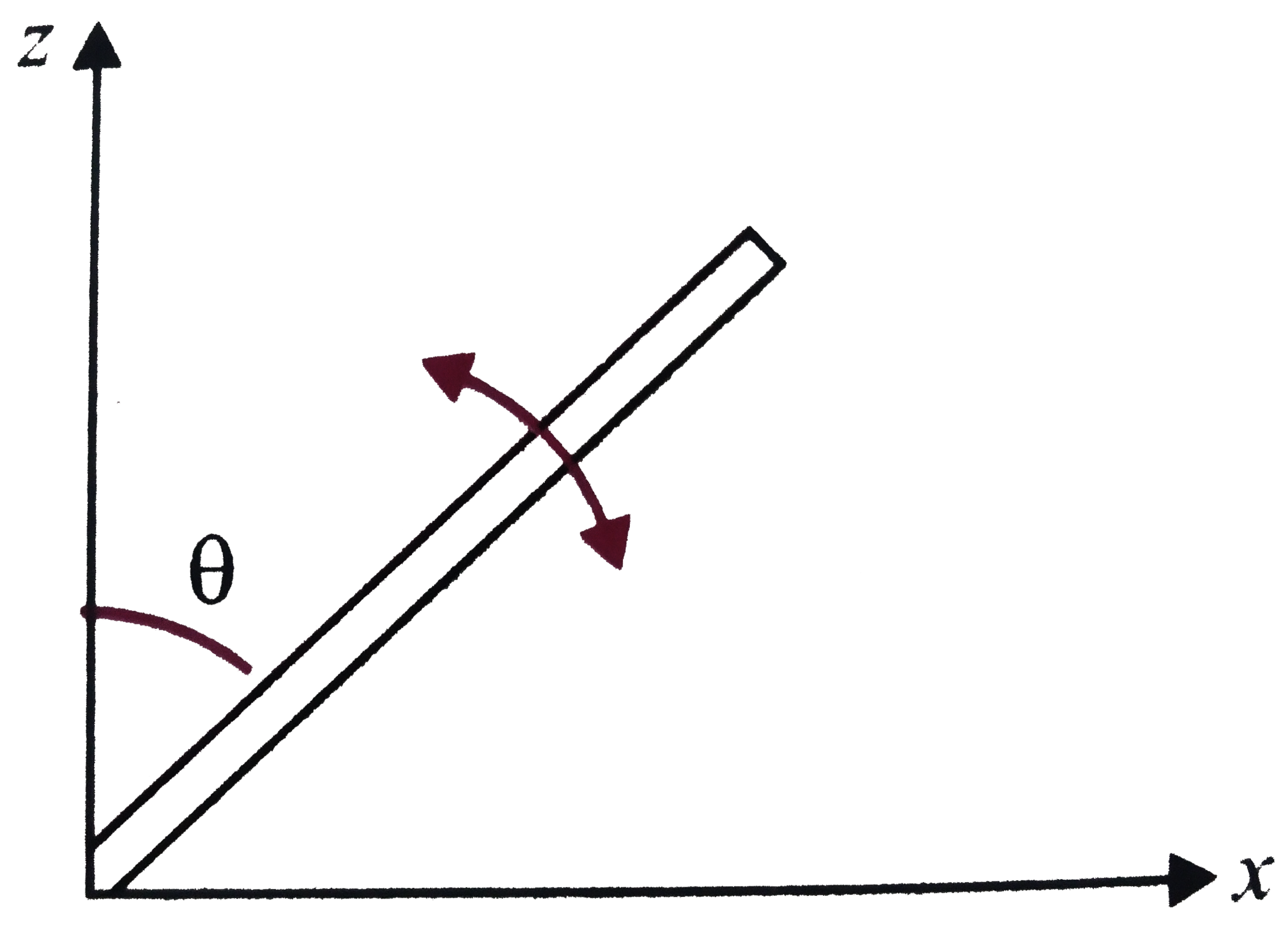 View Solution
View Solution

