A wheel of mass 10 kg has a moment of inertia of 160kg−m2 about its own axis, the radius of gyration will be
10m
8m
6m
4m
The correct Answer is:D
To find the radius of gyration k of the wheel, we can use the relationship between the moment of inertia I, mass m, and radius of gyration k. The formula is given by:
I=m⋅k2
Where:
- I is the moment of inertia,
- m is the mass,
- k is the radius of gyration.
1. Identify the given values:
- Mass m=10kg
- Moment of inertia I=160kg⋅m2
2. Substitute the values into the formula:
160=10⋅k2
3. Rearrange the equation to solve for k2:
k2=16010
4. Calculate k2:
k2=16
5. Take the square root to find k:
k=√16=4m
Final Answer:
The radius of gyration k is 4m.
---
- I is the moment of inertia,
- m is the mass,
- k is the radius of gyration.
- Mass m=10kg
- Moment of inertia I=160kg⋅m2
160=10⋅k2
k2=16010
k2=16
k=√16=4m
The radius of gyration k is 4m.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on kinetic energy, work and power)
30 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on torque, couple)
11 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A wheel of mass 8 kg has moment of inertia equals to 0.5kg-m2. Determine its radius of gyration.
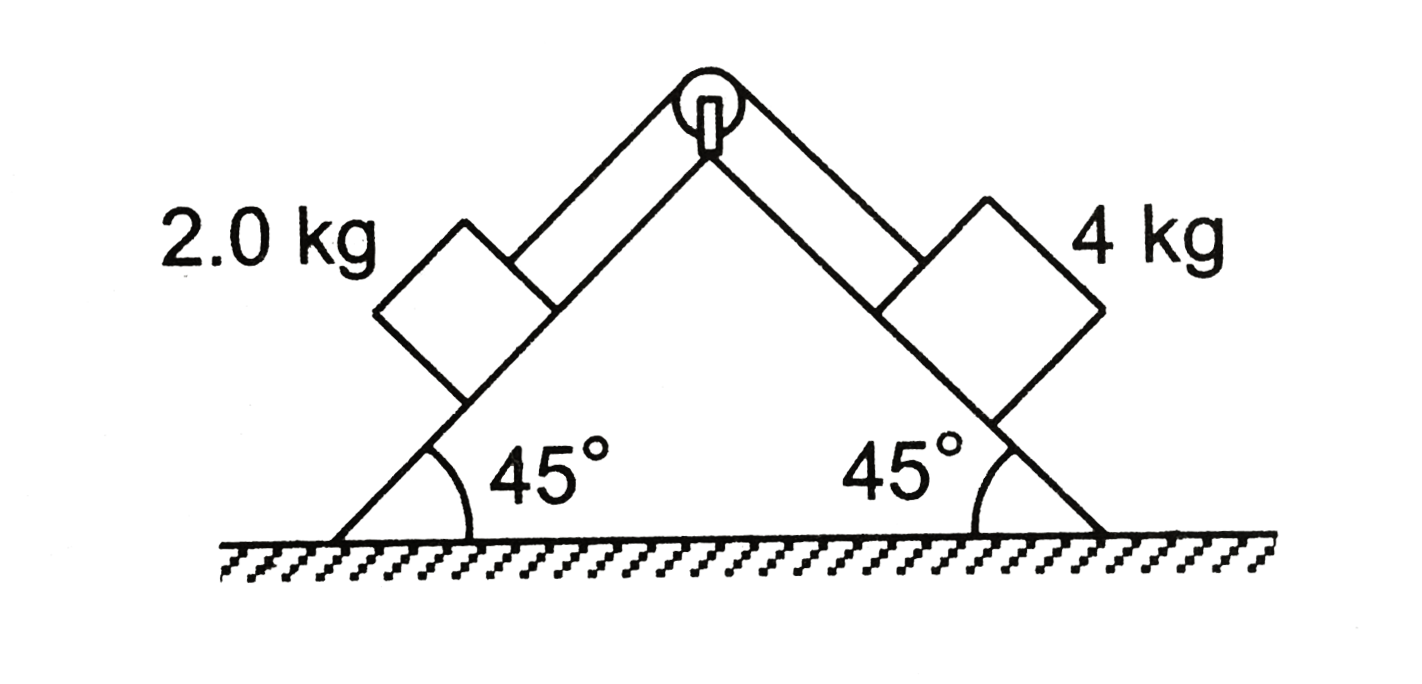
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
View Solution
Knowledge Check
A wheel of mass 15 kg has a moment of inertia of 200 kg m2 about its own axis, the radius of gyration will be
A3.6mB4mC4.6mD1.21mA fly wheel of mass 4 kg has moment of inertia 16kgm2, then radius of gyration about the central axis perpendicular to its plane is
A1mB2mC4mD16mA wheel having moment of inertia 2 kg m2 about its vertical axis, rotates at the rate of 60 rpm about this axis. The torque which can stop the wheel's rotation in one minute would be
A2π15NmBπ12NmCπ15NmDπ18Nm
A wheel having moment of inertia 2kgm2 about its vertical axis, rotates at the rate of 60rom about this axis. The torque which can stop the wheel's rotation in one minuted woould be
View SolutionA wheel having moment of inertia 2kg-m2 about its vertical axis, rotates at the rate of 60 rpm about this axis. The torque which can stop the wheel's rotation in one minute would be
View SolutionA wheel having moment of inertia 4 kg m2 about its axis, rotates at rate of 240 rpm about it. The torque which can stop the rotation of the wheel in one minute is :-
View SolutionIf the moment of inertia of a rigid body is numerically equal to its mass, radius of gyration is
View SolutionA wheel whose radius is R and moment of inertia about its own axis is I, rotates freely about its own axis. A rope is wrapped on the wheel. A body of mass m is suspended from the free end of the rope. The body is released from rest. The velocity of the body after falling a distance h would be:
View Solution
