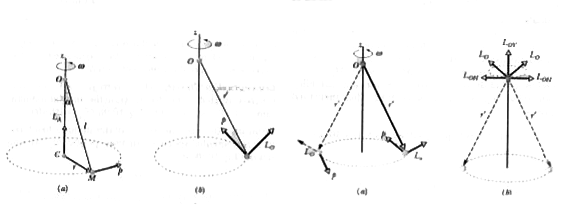
The conical pendulum is in steady circular motion with constant angular velocity ω as shown in Fig. Mass of the particle is M and string makes angle α with vertical.
(a) Find angular momentum of the particle about the center C of the circle and the hinge O about which the string is attached.
(b) Also check whether L is changing or is constant.
(a) Conceptualize/Classify: We start by finding LC, angular momentum of mass M about point C. We can see from Fig. that velocity of the particle is always going to be perpendicular to the line joining particle with the center C. Also, both vectors r and v are lying on horizontal (xy) plane, so the angular momentum, LC will be in the positive z direction. It has magnitude |r⊥||p|=|r||p|=rp, where r is the radius of the circular motion as we can see from Fig.
Calculation: The magnitude of momentum is given by
|p|=Mv=Mrω
The angular momentum about the center C of the circle
LC=r×p
= Mr2ωˆk
Now let us evaluate the angular momentum LO about the point O located at the hinge. From Fig.
→L0=→r×→p
Velocity of the particle is perpendicular to the line OA as shown in the figure.
|LO|=|r.×p||r.||p|=l|p|
or |LO|=Mlrω
where |r.|=l, is the length of the string.
(b) Calculation: We must note that LC is constant, both in magnitude and direction. The magnitude of LO is constant, but its direction is not constant as can be seen from Fig. LO is always perpendicular to the plane containing r. and p. As the particle moves, the plane containing r. and p vector hinges, thus changing the direction of LO at different times. As the bob swings around, LO rotates as shown in fig. The vertical component of LO is not moving, but the horizontal component rotates in the circle with the bob. We can draw the angular momentum at any position we choose, only the magnitude and direction of L have to be same.
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle moves in a circular path with constant speed .Find out a point about which the angular momentum of the particle is constant and another point about which changes with time.
View Solution
Knowledge Check
A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDZero
AmvLBmvlCmvrDZeroA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDzero
AmvLBmvlCmvrDzeroA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
A2ωBω2CωDNot constant
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulum) as shown in the figure. If speed of the particle is constant then,
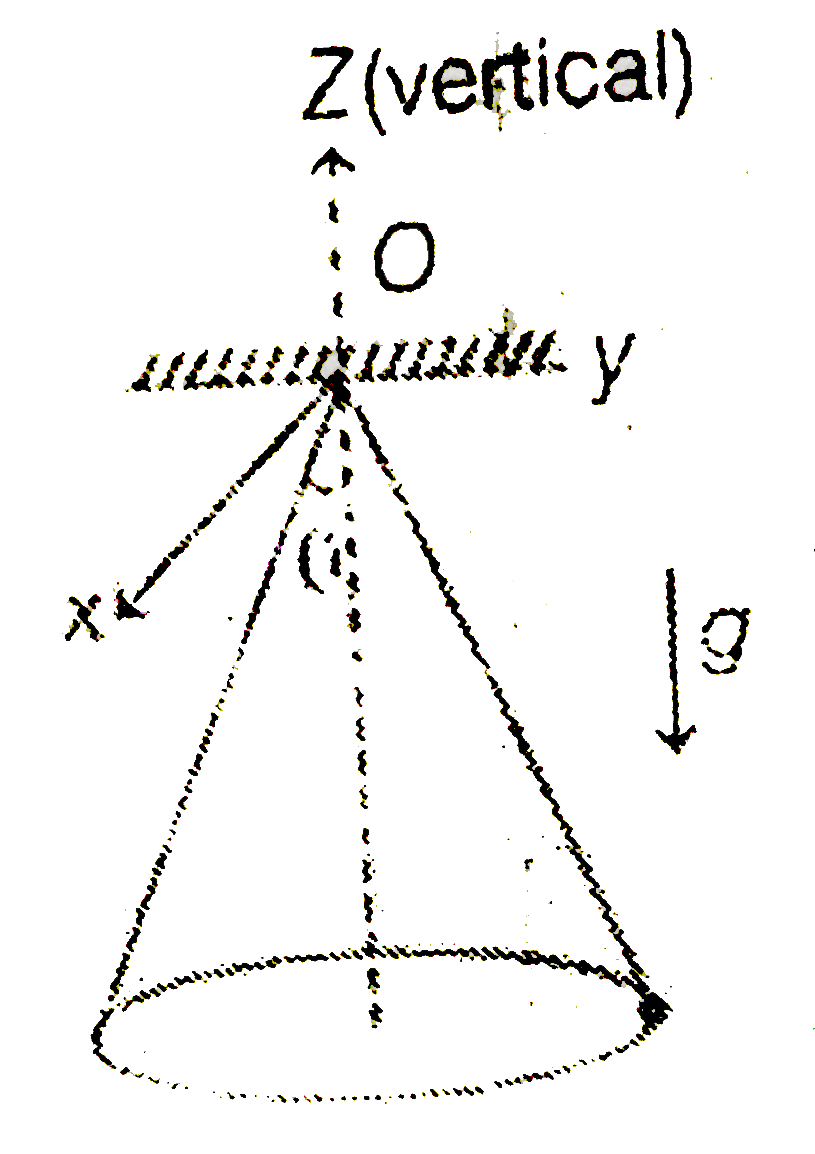
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View Solution
