A rhinoceros beetle rides the rim of a small disk that rotates like a merry-go-round. If the beetle crawls toward the center of the disk, do the following (each relative to the central axis) increase, decrease, or remain the same for the beetle-disk system: (a) rotational inertia, (b) angular momentum, and ( c) angular speed?
(a) Decreases, (b) same (net = 0, so L is conserved), ( c) increases.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS100videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)43videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
A cockroach rides the rim of a rotating merry-go-round. If the angular speed of this system (merry-go-round + cockroach) is constant, does the cockroach have (a) radial acceleration and (b) tangential acceleration? If ω is decreasing, does the cockroach have ( c) radial acceleration and (d) tangential acceleration?
View SolutionIn Fig. a cockroach with mass m rides on a disk of mass 6.00 m and radius R. The disk rotates like a merry-go-round around its central axis at angular speed ωi=1.50rad/s. The cockroach is initially at radius r = 0.800R, but then it crawls out to the rim of the disk. Treat the cockroach as a particle. What then is the angular speed?
View SolutionA cockroach of mass m lies on the rim of a uniform disk of mass 4.00 m that can rotate freely about its center like a merry-goround. Initially the cockroach and disk rotate together with an angular velocity of 0.320 rad/s. Then the cockroach walks halfway to the center of the disk. (a) What then is the angular velocity of the cockroach-disk system? (b) What is the ratio K/K0 of the new kinetic energy of the system to its initial kinetic energy? ( c) What accounts for the change in the kinetic energy?
View SolutionTwo disks are mounted (like a merry-go-round) on low-friction bearings on the same axle and can be brought together so that they couple and rotate as one unit. The first disk, with rotational inertia 3.30kg⋅m2 about its central axis, is set spinning counterclockwise at 450 rev/min. The second disk, with rotational inertia 6.60kg⋅m2 about its central axis, is set spinning counterclockwise at 900 rev/min. They then couple together. (a) What is their angular speed after coupling? If instead the second disk is set spinning clockwise at 900 rev/min, what are their (b) angular speed and (c ) direction of rotation after they couple together?
View Solution[" A bug is on the outer rim of a disk "],[" that has a radius R.The bug walks "],[" towards the center of the disk as it "],[" rotates with an angular velocity w.If "],[" the bug moves with a constant speed "],[" v,how many revolutions does the disk "],[" make before the bug reaches the "],[" center? (Ignore any effects the bug "],[" has on the motion of the disk) "],[[" (A) "2 pi v/ omega R],[" (B) "2 pi omega/Rv]]
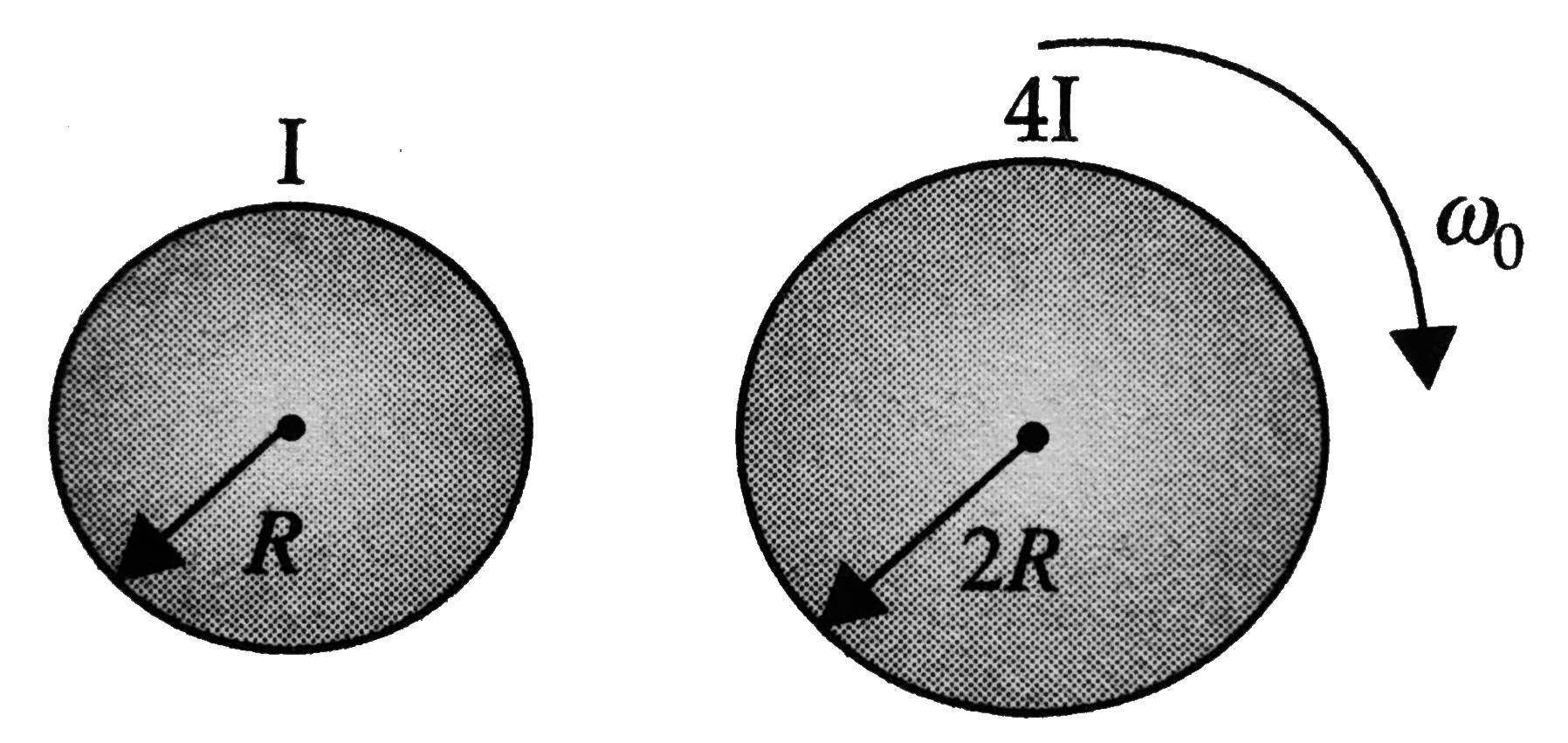
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
 View Solution
View SolutionFigure shows a student, again sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose rotational inertia Iwh about its central axis is 1.2kg⋅m2.
The wheel is rotating at an angular speed ωwh of 3.9 rev/s, as seen from overhead, the rotation is counterclockwise. The axis of the wheel is vertical, and the angular Momentum →Lwh of the wheel points vertically upward.
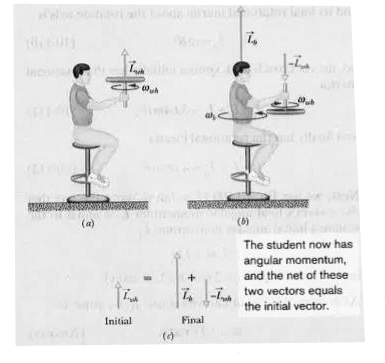
The student now inverts the wheel so that, as seen from overhead, it is rotating clockwise. Its angular momentum is now −→Lwh. The inversion results in the student, the stool, and the wheel's center rotating together as a composite rigid body about the stool's rotation axis, with rotational inertia Ib=6.8kg⋅m2. With what angular speed ωb and in what direction does the composite body rotate after the inversion of the wheel?View SolutionA horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A.View SolutionIn Fig. 10-78, two skaters, each of mass 50 kg, approach each other along parallel paths separated by 3.0 m. They have opposite velocities of 1.4 m/s each. One skater carries one end of a long pole of negligible mass, and the other skater grabs the other end as she passes. The skaters then rotate around the center of the pole. Assume that the friction between skates and ice is negligible. What are (a)the radius of the circle, (b) the angular speed of the skaters, and ( c) the kinetic energy of the two skater system? Next, the skaters pull along the pole unyil they are separated by 1.0 m. What then are (d) their angular speed and (e) the kinetic energy of the system? (f) What provided the energy for the increased kinetic energy?
 View Solution
View SolutionA disk can rotate about its central axis like a merry-go-round. Which of the following pairs of values for its initial and final angular positions, respectively, give a negative angular displacement: (a) -3 rad, +5 rad, (b) -3 rad, -7 rad, ( c) 7 rad, -3 rad?
View Solution

