A 3.0 kg particle-like object moves in a plane with velocity components vx=30m/sandvy=60m/s as is passes through the point with (x, y) coordinates of (3.0, -4.0) m. Just then, in unit vector notation, what is its angular momentum relative to (a) the origin and (b) the point located at (-2.0, -2.0) m?
To solve the problem, we need to calculate the angular momentum of a particle-like object moving in a plane relative to two different points. The object has a mass of 3.0 kg and velocity components vx=30m/s and vy=60m/s. The coordinates of the object at the moment of interest are (3.0,−4.0)m.
Part (a): Angular Momentum Relative to the Origin
1. Determine the position vector r relative to the origin:
r=3^i−4^j
2. Determine the velocity vector v:
v=30^i+60^j
3. Calculate the linear momentum p:
p=mv=3kg⋅(30^i+60^j)=90^i+180^jkg m/s
4. Calculate the angular momentum L using the cross product L=r×p:
L=r×p=(3^i−4^j)×(90^i+180^j)
Using the determinant method for cross products:
L=∣∣
∣
∣∣^i^j^k3−40901800∣∣
∣
∣∣
This results in:
L=(0−0)^i−(0−0)^j+(3⋅180−(−4)⋅90)^k
=(540+360)^k=900^kkg m2/s
Part (b): Angular Momentum Relative to the Point (-2.0, -2.0)
1. Determine the position vector r1 relative to the point (-2, -2):
r1=(3−(−2))^i+(−4−(−2))^j=(3+2)^i+(−4+2)^j=5^i−2^j
2. Use the same velocity vector v as before:
v=30^i+60^j
3. Calculate the angular momentum L1 using the cross product L1=r1×p:
L1=r1×p=(5^i−2^j)×(90^i+180^j)
Using the determinant method for cross products:
L1=∣∣
∣
∣∣^i^j^k5−20901800∣∣
∣
∣∣
This results in:
L1=(0−0)^i−(0−0)^j+(5⋅180−(−2)⋅90)^k
=(900+180)^k=1080^kkg m2/s
Final Answers
- (a) Angular momentum relative to the origin: L=900^kkg m2/s
- (b) Angular momentum relative to the point (-2, -2): L1=1080^kkg m2/s
r=3^i−4^j
v=30^i+60^j
p=mv=3kg⋅(30^i+60^j)=90^i+180^jkg m/s
L=r×p=(3^i−4^j)×(90^i+180^j)
L=∣∣
∣
∣∣^i^j^k3−40901800∣∣
∣
∣∣
L=(0−0)^i−(0−0)^j+(3⋅180−(−4)⋅90)^k
=(540+360)^k=900^kkg m2/s
r1=(3−(−2))^i+(−4−(−2))^j=(3+2)^i+(−4+2)^j=5^i−2^j
v=30^i+60^j
L1=r1×p=(5^i−2^j)×(90^i+180^j)
L1=∣∣
∣
∣∣^i^j^k5−20901800∣∣
∣
∣∣
L1=(0−0)^i−(0−0)^j+(5⋅180−(−2)⋅90)^k
=(900+180)^k=1080^kkg m2/s
- (a) Angular momentum relative to the origin: L=900^kkg m2/s
- (b) Angular momentum relative to the point (-2, -2): L1=1080^kkg m2/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)43videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT18videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
A motorbike starts from the origin and moves over an xy plane with acceleration components ax=6.0m/s2anday=−3.0m/s2. The initial velocity of the motorbike has components v0x=12.0m/sandv0y=18.0m/s. Find the velocity of the motorbike, in unt-vector notation, when it reaches its greatest y coordinate.
View SolutionA particle starts from the origin at t=0 with a velocity of 8.0ˆjm/s and moves in the x-y plane with a constant acceleration of (4.0ˆi+2.0ˆj)m/s2. At the instant the particle's x-coordinate is 29 m, what are
(a) its y-coordinate and
(b) its speed ?View Solution
Knowledge Check
- Question 1 - Select One
A 2.0-kg projectile is fired with initial velocity components vox=30m/s and voy=40m/s from a point on the earth's surface. Neglect any effects due to air resistance.
What is the kinetic energy of the projectile when it reaches the highest point in its trajectory ?AzerojoulesB1600JC900JD2500J - Question 2 - Select One
A 2.0-kg projectile is fired with initial velocity components vox=30m/s and voy=40m/s from a point on the earth's surface. Neglect any effects due to air resistance.
How much work was done in firing the projectile ?A900JB2500JC1600JD4900J - Question 3 - Select One
The point (x,y) lies on the line with slope m and passes through the fixed point (x0,y0) if and only if its coordinates satisfy the equation y−y0 is equal to
Am(x−x0)Bm(y−x0)Cm(y−x)Dm(x−y0)
Force →F=(2.0N)ˆi−(3.0N)ˆk acts on a pebble with position vector →r=(0.50m)ˆj−(2.0m)ˆk relative to the origin. In unit-vector notation, what is the resulting torque on the pebble about the origin ?
View SolutionTwo particles A and B are moving in the x−y plane such that their velocity components are vx=1m/s,vy=1√3m/s (for A) and vx=2m/s,vy=2m/s (for B). If both the particles start moving from the same point, what is the angle between their paths ?
View SolutionDistance of point P on the curve y=x3/2 which is nearest to the point M (4, 0) from origin is
View SolutionA particle starts from the point (0m,8m) and moves with uniform velocity of 3ˆim/s. After 5 seconds, the angular velocity of the particle about the origin will be :
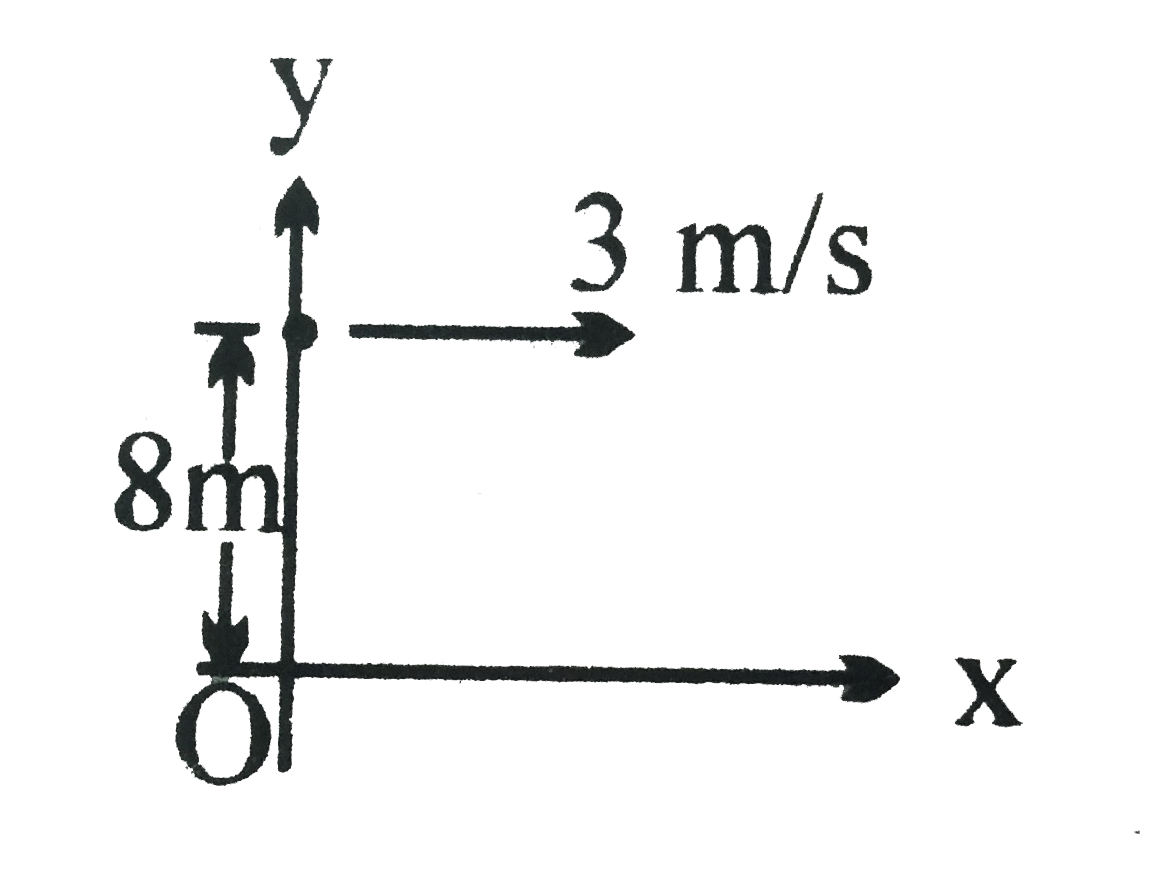 .View Solution
.View SolutionA body of mass 3 kg is moving along the line 5y= 12x +39 with a velocity 5 m/s. At t=0, it is at the point (-2, 3). Find the angular momentum of the particle at t =5 s.
View Solution

