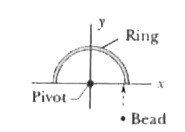
Figure 10-82 is an overhead view of semicircular ring of mass m and radius R that lies on a frictionless surface. The ring is connected by elevated spokes (not shown) to a pivot at the center of the semicircle. The ring can rotate around that pivot but is initially stationary. A bead of mass m and speed v is shot into the ring, entering under the spokes and tangentially to the ring and then sliding along the ring. The ring and bead then rotate together around the pivot. Find their angular speed.

Video Solution

Text Solution

Verified by Experts

v/2R

|

Class 12 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

For a uniform ring of mass M and radius R at its centre
Afield and potential both are zero
Bfield is zero but potential is $\frac{G M}{R}$
Cfield is zero but potential is $- G M / R$
Dmagnitude of field is $\frac{G M}{R^{2}}$ and potential $- \frac{G M}{R}$
The total energy of rolling ring of mass m and radius R is
A $3 / 2 m v^{2}$
B $1 / 2 m v^{2}$
C $m v^{2}$
D $5 / 2 m v^{2}$
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $\frac{5}{2} M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{1}{2} M R^{2}$
D $M R^{2}$

RESNICK AND HALLIDAY-RIGID BODY DYNAMICS - I-PROBLEMS

Home
Ask Doubt
Profile