A marble and a cube are placed at the top of a ramp. Starting from rest at the same height, the marble rolls and the cube slides (no kinetic friction) down the ramp. Determine the ratio of the center-of-mass speed of the cube to the center-of-mass speed of the marble at the bottom of the ramp.
1.14
1.20
0.707
1.18
The correct Answer is:D
To solve the problem, we need to analyze the motion of both the marble and the cube as they descend the ramp. We will use the principles of energy conservation to find the center-of-mass speeds of both objects at the bottom of the ramp.
Step 1: Understand the System
Both the marble and the cube start from rest at the same height h on the ramp. The marble rolls down while the cube slides down without friction.
Step 2: Apply Conservation of Energy for the Cube
For the cube, which slides down without any rotation, the potential energy at the top is converted entirely into translational kinetic energy at the bottom.
- Potential Energy at the top:
PEcube=mgh
- Kinetic Energy at the bottom:
KEcube=12mv2c
- Setting potential energy equal to kinetic energy:
mgh=12mv2c
- Simplifying, we find:
gh=12v2c⟹v2c=2gh⟹vc=√2gh
Step 3: Apply Conservation of Energy for the Marble
For the marble, which rolls down the ramp, both translational and rotational kinetic energy need to be considered.
- Potential Energy at the top:
PEmarble=mgh
- Kinetic Energy at the bottom:
KEmarble=12mv2m+12Iω2
- For a solid sphere, the moment of inertia I is given by I=25mr2 and the relationship between linear velocity vm and angular velocity ω is vm=rω. Thus, ω=vmr.
- Substituting I and ω into the kinetic energy equation:
KEmarble=12mv2m+12(25mr2)(vmr)2
=12mv2m+15mv2m=12mv2m+210mv2m=710mv2m
- Setting potential energy equal to total kinetic energy:
mgh=710mv2m
- Simplifying, we find:
gh=710v2m⟹v2m=107gh⟹vm=√107gh
Step 4: Calculate the Ratio of Speeds
Now we can find the ratio of the center-of-mass speed of the cube to that of the marble:
vcvm=√2gh√107gh=
⎷2gh107gh=√2⋅710=√1410=√1.4
Calculating this gives:
√1.4≈1.18
Final Answer
The ratio of the center-of-mass speed of the cube to that of the marble is approximately 1.18.
Both the marble and the cube start from rest at the same height h on the ramp. The marble rolls down while the cube slides down without friction.
For the cube, which slides down without any rotation, the potential energy at the top is converted entirely into translational kinetic energy at the bottom.
PEcube=mgh
- Kinetic Energy at the bottom:
KEcube=12mv2c
- Setting potential energy equal to kinetic energy:
mgh=12mv2c
- Simplifying, we find:
gh=12v2c⟹v2c=2gh⟹vc=√2gh
For the marble, which rolls down the ramp, both translational and rotational kinetic energy need to be considered.
PEmarble=mgh
- Kinetic Energy at the bottom:
KEmarble=12mv2m+12Iω2
- For a solid sphere, the moment of inertia I is given by I=25mr2 and the relationship between linear velocity vm and angular velocity ω is vm=rω. Thus, ω=vmr.
KEmarble=12mv2m+12(25mr2)(vmr)2
=12mv2m+15mv2m=12mv2m+210mv2m=710mv2m
mgh=710mv2m
- Simplifying, we find:
gh=710v2m⟹v2m=107gh⟹vm=√107gh
Now we can find the ratio of the center-of-mass speed of the cube to that of the marble:
vcvm=√2gh√107gh=
⎷2gh107gh=√2⋅710=√1410=√1.4
Calculating this gives:
√1.4≈1.18
The ratio of the center-of-mass speed of the cube to that of the marble is approximately 1.18.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS100videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
A uniform cube of mass M and side length a is placed at rest at the edge of a table. With half of the cube overhanging from the table, the cube begins to roll off the edge. There is sufficient friction at the edge so that the cube does not slip at the edge of the table. Find -
(a) the angle θ0 through which the cube rotates before it leaves contact with the table.
(b) the speed of the centre of the cube at the instant it breaks off the table.
(c) the rotational kinetic energy of the cube at the instant its face AB becomes horizontal.
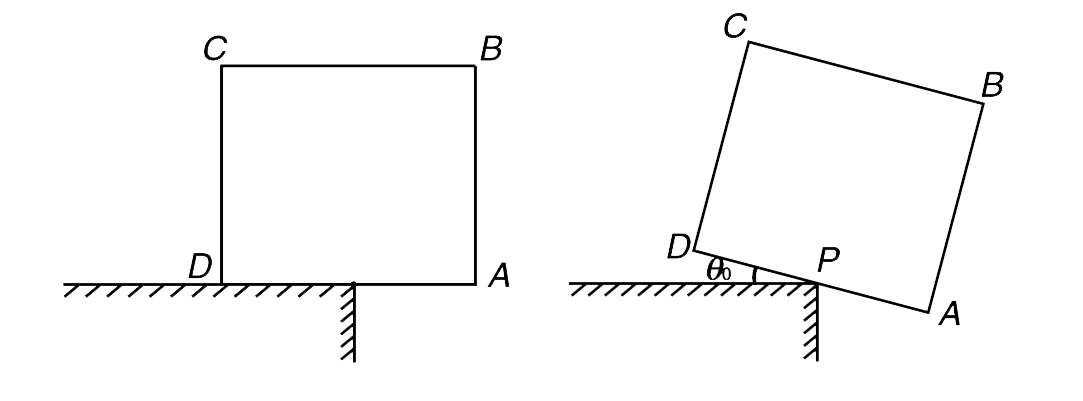 View Solution
View SolutionA cube of mass m and height H slides with a speed v. It strikes the obstacle of height h=(H4). Find the speed of the CM of the cube just after the collision.
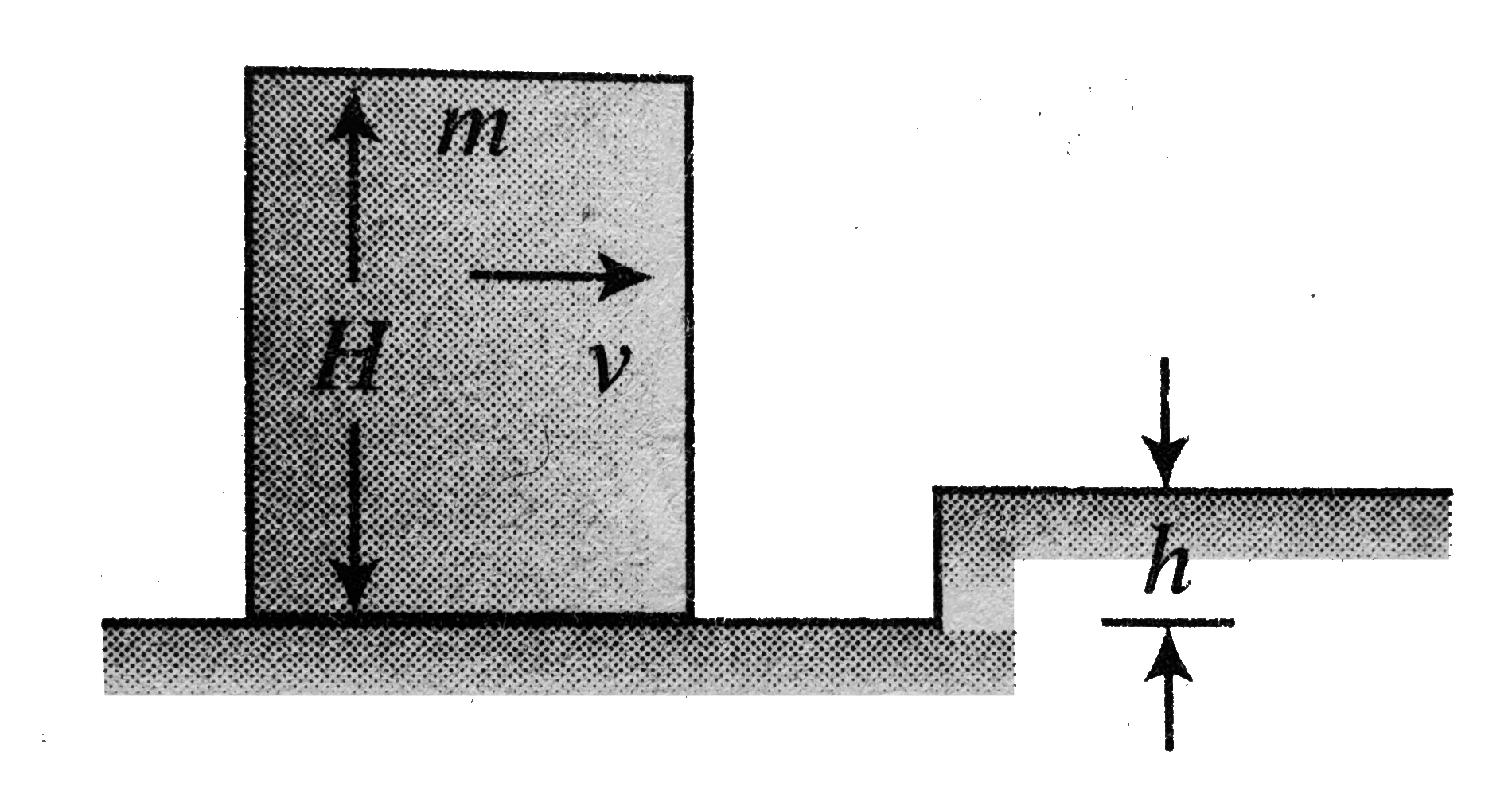 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cube of mass M starts of rest from point 1 at a height 4R, where R is the radius of the circular track. The cube slides down the frictionless track and around the loop. The force which the track exerts on the cube at point 2 is :
 A3 MgBMgC2MgDCube will not reach the point 2
A3 MgBMgC2MgDCube will not reach the point 2 - Question 2 - Select One
A solid sphere starts from rest at the top of an incline of height h and length l, and moves down. The force of friction between the sphere and the incline is F. This is insufficient to prevent slipping. The kinetic energy of the sphere at the bottom of the incline is W.
AThe work done against the force of friction is Fl.BThe heat produced is Fl.CW=mgh-FlDW>(mgh-Fl) - Question 3 - Select One or More
A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by
Athe work done against the frictional force is Fl.Bthe heat produced is F l.CW = mgh - F lDW gt (mgh - F l)
A solid cylinder with base radius jis placed on top of an inclined plane of length land slope angle α (Fig). The cylinder rolls down without slipping. Find the speed of the centre of mass of the cylinder at the bottom of the plane, if the coefficient of rolling friction is k. Can rolling friction be neglected? Do the calculation for the following conditions: l=1m,α=30∘,r=10cm,k=5×10−4m . What would be the speed if, in the absence of friction, the cylinder slides down?
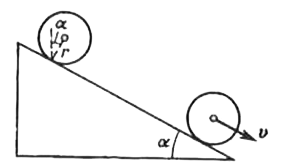 View Solution
View SolutionA person of mass 75kg works in a where his job is to arrange heavy articles in a stone - room As shown in figure he place a packing of mass 20kg on a ramp that is inclined to the horizontal at 37∘ and pushed it up the ramp with an acceleration 1.5ms−2 .This is the minimum acceleration for the packege to reach the top to the ramp.THe coefficient of static and friction between the shoes of the person and the ground is 0.8 and coefficient of kinetic friction for the motion of package on the is 0.5

Force of friction acting on the person is
Now suppose that the ground is wet which reduces the coefficient of static friction between the shoes of the person and the ground of 0.2 (other value remaining unchanged) Answer the following question:View SolutionTwo cubes A and B of same shape, size and mass are placed on a rough surface in the same manner. Equal forces are applied on the both cubes. But at the cube A, the force is applied at the top in horizontal direction. But at the cube B just above the center of mass of the cube in the same manner. Then,
View SolutionTwo objects, a ring and a spherical shell of same mass and radius are released from the top of two Identical inclined plane. If they are rolling without slipping, then ratio of speed of center of mass of the two objects when they will reach the bottom of the inclined plane is
View SolutionAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
View Solution

