Question

In the determination of molecular mass by Victor - Meyer's Method 0.790 g of a volatile liquid displaced $1.696\times {10}^{-4}{m}^3$ of moist air at 303 K and at $1\times {10}^{5}N{m}^{-2}$ pressure. Aqueous tension at 303 K is $4.242\times {10}^{3}N{m}^{-2}$ . Calculate the molecular mass and vapour density of the compound .

Explanation

Mass of the organic compound =0.79 g
Volume of Vapour = `V_1 = 1.696 xx 10^(-4) m^(3)`
Volume of air displaced = Volume of vapour.
`P_1 `= ( atmospheric pressure - aqueous tension )
`=(1.0 xx 10^5) - (4.242 xx 10^(3)) = 0.958 xx 10^(5) Nm^(-2)`
`T_1 `= 303 K

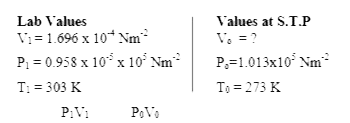
`(P_1 V_1)/( T_1) = (P_0 V_0)/( T_0)`
`V_0 = (P_1 V_1 T_0)/(P_0 T_1)`
`V_0 = (0.958 xx 10^(5) xx 1.696 xx 10^(-4))/(1.013 xx 10^(3)) xx (273)/(303)`
`V_0 = 1.445 xx 10^(-4) m^3`
The mass of `1.445 xx 10^(-4)m^(3)` of vapour at S.T.P= 0.79 g .
The mass of ` 2.24 xx 10^(-2) m^(3)` of vapour of S.T.P is
`= (2.24 xx 10^(-2) xx 0.79)/( 1.445 xx 10^(-4))`
The molecular mass of the substance = 122 .46
Vapour density of the compound `=(" molecular mass ")/(2)`
`= (122.46)/(2) = 61.23`