In the determination of molecular mass by Victor - Meyer's Method 0.790 g of a volatile liquid displaced of moist air at 303 K and at pressure. Aqueous tension at 303 K is . Calculate the molecular mass and vapour density of the compound . Solution in Gujrati
Mass of the organic compound =0.79 g
Volume of Vapour =
Volume of air displaced = Volume of vapour.
= ( atmospheric pressure - aqueous tension )
= 303 K
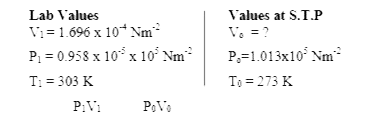
The mass of of vapour at S.T.P= 0.79 g .
The mass of of vapour of S.T.P is
The molecular mass of the substance = 122 .46
Vapour density of the compound
Topper's Solved these Questions
- CHEMICAL CALCULATION Book:NCERT GUJARATIChapter:CHEMICAL CALCULATION Exercise:EXAMPLE
Explore 3 Videos
- CHEMICAL CALCULATION Book:NCERT GUJARATIChapter:CHEMICAL CALCULATION Exercise:Problems of Practice
Explore 43 Videos
- CHEMICAL CALCULATION Book:NCERT GUJARATIChapter:CHEMICAL CALCULATION Exercise:Question ( Answer the following )
Explore 7 Videos
- CHEMICAL BONDINGBook:NCERT GUJARATIChapter:CHEMICAL BONDINGExercise:Questions(E. Explain briefly on the following)
Explore 1 Video
- CHEMICAL EQUILIBRIUM - IBook:NCERT GUJARATIChapter:CHEMICAL EQUILIBRIUM - IExercise:Questions(E. Explain briefly on the following)
Explore 2 Videos
Similar Questions
Calculate the mass of CO2 that would be obtained by completely dissolving 10 kg of pure CaCO3 in HCl.
CaCO3+2HCl→CaCl2+H2O+CO2
View SolutionCalculate the formula weight of compounds NO2
View SolutionCan two different compounds have same molecular formula ? Illustrate your answer with two examples.
View SolutionCalculate the lattice enthalpy of CaCl2 given that the enthalpy of :
i) Sublimation of Ca in 121.8 kJ mol−1
ii) Dissociation of Cl2 to 2Cl is 242.8 kJ mol−1
iii) Ionisation of Ca to Ca2+ is 2422 kJ mol−1
iv) Electron gain for Cl to Cl− is - 355 kJ mol−1
v) ΔH(o)f overall is −795 kJ mol−1
View SolutionTwo moles of H2 and three moles of I2 are taken in 2dm3 vessel and heated. If the equilibrium mixture contains 0.8 moles of HI, calculate KpandKc for the reaction
H2(g)+I2(g)⇔2HI(g)
View SolutionThe vapour pressure of benzene is 1.53 xx 10^(4) Nm^(-2) at 303 K and 5.2 xx 10^(4) Nm^(-2) at 333 K. Calculate the mean latent heat of evaportion of benzene over this temprature range
View Solution10g of cane sugar (molecular mass = 342) in 1 xx 10^(-3) m^(3) of solution produces an osmotic pressure of 6.68 xx 10^(4) Nm^(-2) at 273 K. Calculate the value of S in SI units.
View SolutionCalculate the mass and density of the earth. Given that Gravitational constant G=6.67×10−11Nm2/kg2, the radius of the earth =6.37×106m and g =9.8m/s2.
View SolutionAn ideal gas expands from the volume of 1×10−3m3 to 1×10−2m3 at 300K against a constant pressure at 1×105Nm−2 . The work done is
View SolutionIn the Victor Meyer's method for the determination of molecular mass of an organic compound, what is measured ?
View SolutionIn the determination of molecular mass by Victor - Meyer's Method 0.790 g of a volatile liquid displaced 1.696×10−4m3 of moist air at 303 K and at 1×105Nm−2 pressure. Aqueous tension at 303 K is 4.242×103Nm−2 . Calculate the molecular mass and vapour density of the compound .
View SolutionIn the determination of molecular mass by Victor - Meyer's Method 0.790 g of a volatile liquid displaced 1.696×10−4m3 of moist air at 303 K and at 1×105Nm−2 pressure. Aqueous tension at 303 K is 4.242×103Nm−2 . Calculate the molecular mass and vapour density of the compound .
View SolutionIn the determination of molecular mass by Victor - Meyer's Method 0.790 g of a volatile liquid displaced 1.696 xx 10^(-4) m^(3) of moist air at 303 K and at 1 xx 10^(5) Nm^(-2) pressure. Aqueous tension at 303 K is 4.242 xx 10^(3) Nm^(-2) . Calculate the molecular mass and vapour density of the compound .
View SolutionIn the determination of molecular mass by Victor - Meyer's Method 0.790 g of a volatile liquid displaced 1.696 xx 10^(-4) m^(3) of moist air at 303 K and at 1 xx 10^(5) Nm^(-2) pressure. Aqueous tension at 303 K is 4.242 xx 10^(3) Nm^(-2) . Calculate the molecular mass and vapour density of the compound .
View SolutionThe rms speed of the molecules of a gas of density 4 kg m^(-3) and pressure 1.2 xx 10^5 Nm^(-2) is :
View Solution