Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
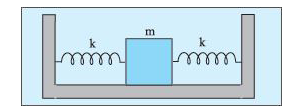 Solution in Bengali
Solution in Bengali
Let the mass be displaced by a small distance x to the right side of the equilibrium position, as shown in Fig. 14.15. Under this situation the spring on the left side gets
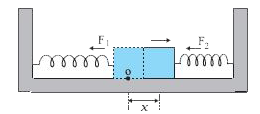
elongated by a length equal to x and that on the right side gets compressed by the same length. The forces acting on the mass are then,
F1=−kx (force exerted by the spring on the left side, trying to pull the mass towards the mean position)
F2=−kx (force exerted by the spring on the right side, trying to push the mass towards the mean position)
The net force, F, acting on the mass is then given by,
F=−2kx
Hence the force acting on the mass is proportional to the displacement and is directed towards the mean position, therefore, the motion executed by the mass is simple harmonic. The time period of oscillations is,
T=2π√m2k
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercises
27 Videos
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
3 Videos
Similar Questions
Which of the following examples represent periodic motion?
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
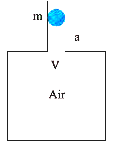
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
View SolutionThe instantaneous speed of the point of contact during rolling is zero.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
