Take any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
To solve the problem, we need to analyze the inequalities involving the lengths of segments formed by a point O inside triangle PQR. We will use the triangle inequality theorem, which states that in any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side.
1. Consider the triangle PQR and point O inside it.
- We have triangle PQR with vertices P, Q, and R, and point O located inside this triangle.
2. Evaluate the first inequality: OP + OQ > PQ.
- We can form triangle OPQ using the segments OP, OQ, and PQ.
- According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Here, we have:
OP+OQ>PQ
- Therefore, the first inequality is true.
3. Evaluate the second inequality: OQ + OR > QR.
- Now, consider triangle OQR formed by segments OQ, OR, and QR.
- Again, applying the triangle inequality:
OQ+OR>QR
- Thus, the second inequality is also true.
4. Evaluate the third inequality: OR + OP > RP.
- Finally, we look at triangle OPR formed by segments OR, OP, and RP.
- Using the triangle inequality once more:
OR+OP>RP
- Hence, the third inequality is also true.
Conclusion:
All three inequalities hold true:
(i) OP+OQ>PQ
(ii) OQ+OR>QR
(iii) OR+OP>RP
- We have triangle PQR with vertices P, Q, and R, and point O located inside this triangle.
- We can form triangle OPQ using the segments OP, OQ, and PQ.
- According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Here, we have:
OP+OQ>PQ
- Therefore, the first inequality is true.
- Now, consider triangle OQR formed by segments OQ, OR, and QR.
- Again, applying the triangle inequality:
OQ+OR>QR
- Thus, the second inequality is also true.
- Finally, we look at triangle OPR formed by segments OR, OP, and RP.
- Using the triangle inequality once more:
OR+OP>RP
- Hence, the third inequality is also true.
All three inequalities hold true:
(i) OP+OQ>PQ
(ii) OQ+OR>QR
(iii) OR+OP>RP
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.5
8 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.1
1 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - SOLVED EXAMPLES
6 Videos
- SYMMETRYBOOK - NCERTCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.1
9 Videos
Similar Questions
Take any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
View SolutionS in any point on side QR of a ΔPQR.ShowtˆPQ + QR+RP gt 2PS.
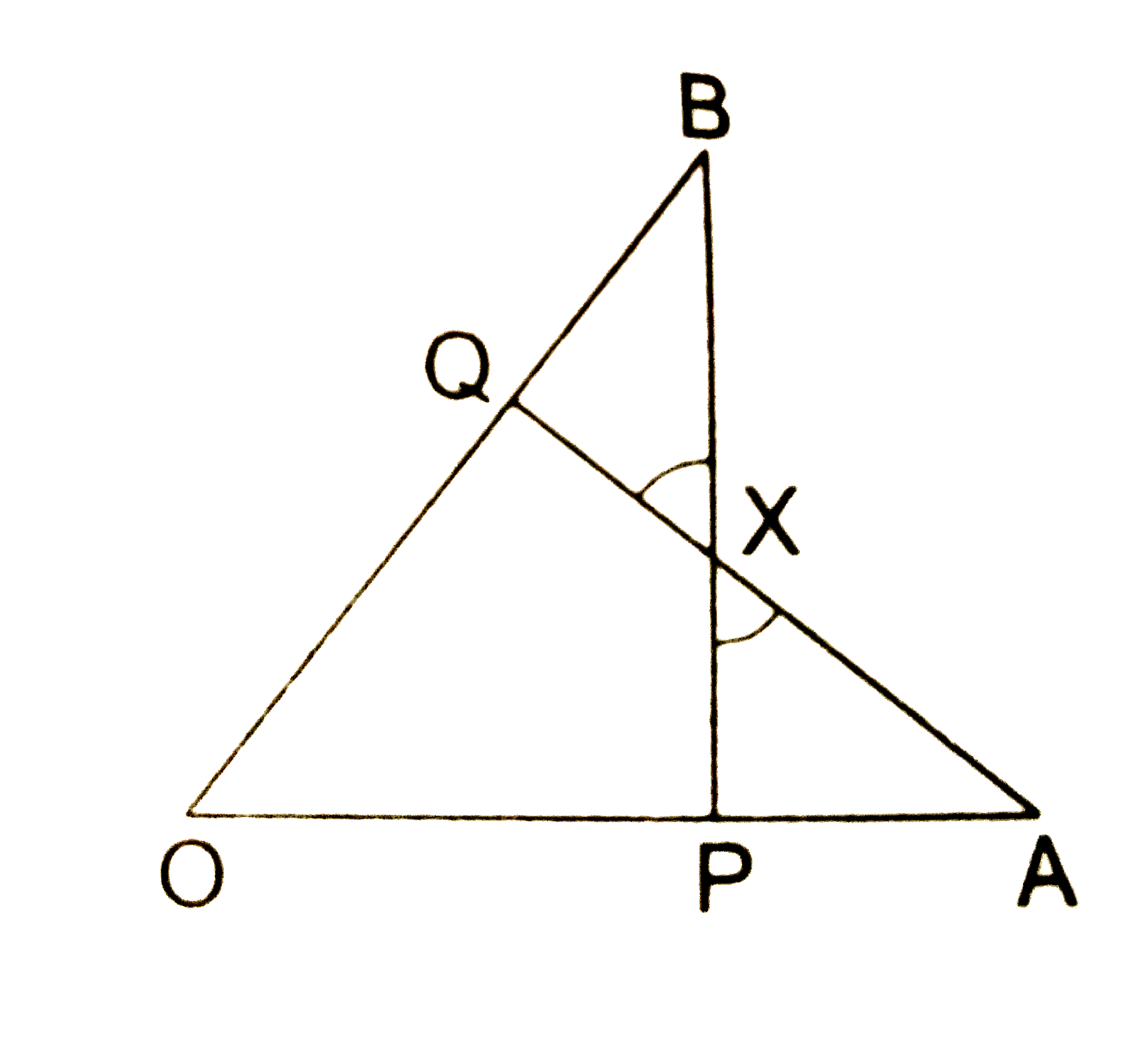
View SolutionIn the givne figure, OA = OB and OP = OQ.
Prove that (i) PX = QX, (ii) AX = BX.
View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS.
View SolutionO is a point in the interior of ∠PQR such that OM⊥QRandON⊥QP ,if ∠PQR=60∘, then find the value of ∠NOM.
View SolutionIn the given figure, OA=OB and OP=OQ. Prove that (i) PX=QX, (ii) AX=BX
View SolutionConsider a circle with centre at C. Let OP, OQ denote respectively the tangents to the circle drawn from a point o outside the circle. Let R be a point on OP and S be a point on OQ such that OR×SQ=OS×RP. Which of the following statements is/are correct?
1. If X is the circle with centre at O and radius OR, and Y is the circle with centre at O and radius OS, then X = Y.
2. ∠POC+∠QCO=90∘
Select the correct answer using the code given below.
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionIn the figure, P is the point of contact.
If OP=7.2,OQ=3.2, find OR and QR.

View SolutionAngles QandR of a ΔPQR are 25∘and65∘. Write which of the following is true : (i) PQ2+QR2=RP2 (ii) PQ2+RP2=QR2 ( iii) RP2+QR2=PQ2
View Solution
