Given two circles x2+y2+3√2(x+y)=0 and x2+y2+5√2(x+y)=0. Let the radius of the third circle, which touches the two given circles and to their common diameter, be 2λ−1λ The value of λ is
10
8
7
5
The correct Answer is:B
Let C1andC2 be the centres of the circles x2+y2=3√2(x+y)=0andx2+y2+5√2(x+y)=0 and let their radii be r1andr2 respetively. Then,
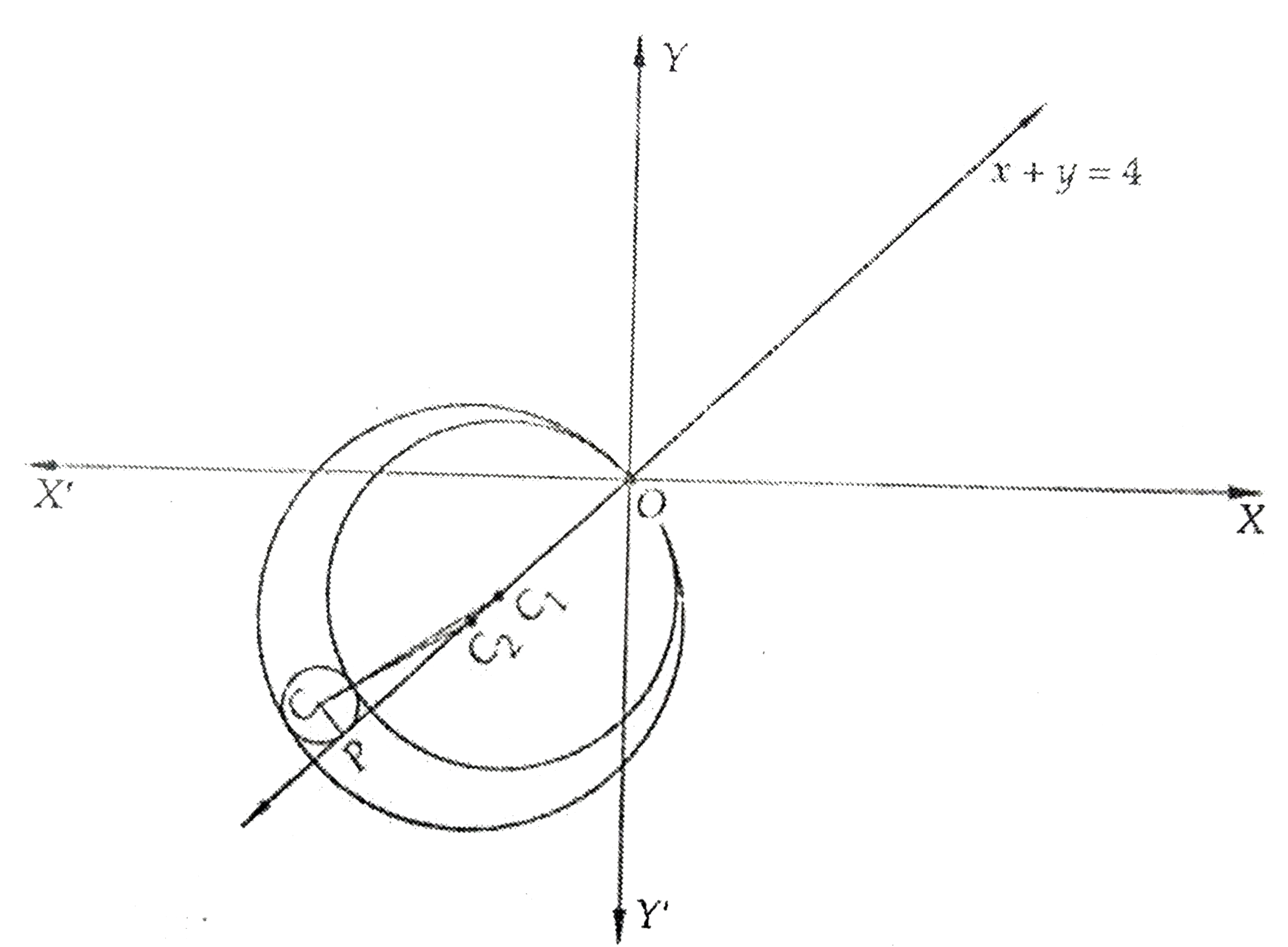
C1(−3√2,−3√2),C2(−5√2,−5√2),r1=3andr2=5
Let C be the centre and r be the radius of the circle touching the given circles and their common diameter at point P. Then,
CC21=CP2+C1P2
⇒(r+r1)2=r2+(C1C2+C2P)2
⇒(r+r1)2=r2+(C1C2+√CC22−CP2)2
⇒(r+r1)2=r2+{(r2−r1)+√(r2−r)2−r2}2
⇒(3+r)2=r2+{(2+√(5−r)2−r2}2
⇒9+6r=(2+√25−10r)2
⇒9+6r=4+25−10r+4√25−10r
⇒(4r−5)2=25−10r⇒16r2−30r=0⇒r=158
∴2λ−1λ=158⇒λ=8
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Let the equation of the circle is x2+y2=25 and the equation of the line x+y=8. If the radius of the circle of maxium area and also touches x+y=8 and x2+y2=25 is 4√2+5λ. Then the value of λ is.
View SolutionIf a circle passes through the points of intersection of the coordinate axes with the lines λx−y+1=0 and x−2y+3=0, then the value of λ is............
View Solution
Knowledge Check
If the two straight lines 3x−2y−8=0 and 2x−y−5=0 lie along two diameters of a circle which touches the x-axis then the equation of the circle is
A(x−2)2+(y−1)2=1B(x+2)2+(y−1)2=1C(x−2)2+(y+1)2=1DnoneIf the two circles (x−2)2+(y+3)2=λ2 and x2+y2−4x+4y−1=0 intersect in two distinct points then :
Aλ<−2B−2<λ<4C2<λ<4Dλ=−2
Find the equation of a circle of radius 5 which lies within the circle x2+y2+14x+10y−26=0 and which touches the given circle at the point (−1,3).
View SolutionThe equation of a circle is x2+y2=4. Find the center of the smallest circle touching the circle and the line x+y=5√2
View SolutionIf 2x-3y=0 is the equation of the common chord of the circles x2+y2+4x=0 and x2+y2+2λy=0 then the value of λ is
View SolutionIf 2x−3y=0 is the equation of the common chord of the circles, x2+y2+4x=0 and x2+y2+2λy=0, then the value of λ is
View SolutionIf the circle x2+y2−4x−6y+λ=0 touches the axis of x , then determine the value of λ and the point of contact
View SolutionIf the line y=3x+λ touches the hyperbola 9x2−5y2=45, then the value of λ is
View Solution
