In example 104, area of ΔPQ2Q3, in square units is
6√2
4√2
8√2
3√2
The correct Answer is:A
Area of
ΔPQ2Q3=12(Q2Q3×√2)=12×12×√2=6√2 sq. units
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
ABCD is rectangle. P and Q are points on ABandBC respectively such that the area of triangle APD=5, area of triangle PBQ=4 and area of triangle QCD=3, all areas in square units. Then the areaof the triangle DPQ in square units is
View SolutionThe largest possible square is inscribed in a circle of 2π units circumference. The area of the square in square units is
View Solution
Knowledge Check
If the end points of the diameter of a circle are (-2 , 3) and (6 , -3) , then the area of the circle ( in square units ) is _______
A5503B5407C5607D5507The largest possible square is inscribed in a circle of 2π units circumference. The area of the square in square units is
A4π√2B2π√2C√2D2In the figure below, all of the small square are equal in area, and the area of rectangle ABCD is 1 square unit. Which of the following expressions represents the area, in square units, of the shaded region?
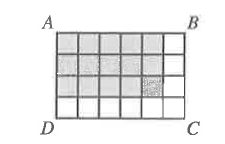 A16⋅14B16⋅34C16⋅56D56⋅34
A16⋅14B16⋅34C16⋅56D56⋅34
The total area of the non-triangle regions in the figure below (the shaded area) is equal to (pq) square units, where p and q are coprime natural numbers then p+q is equal to
View SolutionThe diagonal of a square is 'a' units .Then , the area of the square is ________ square units .
View Solution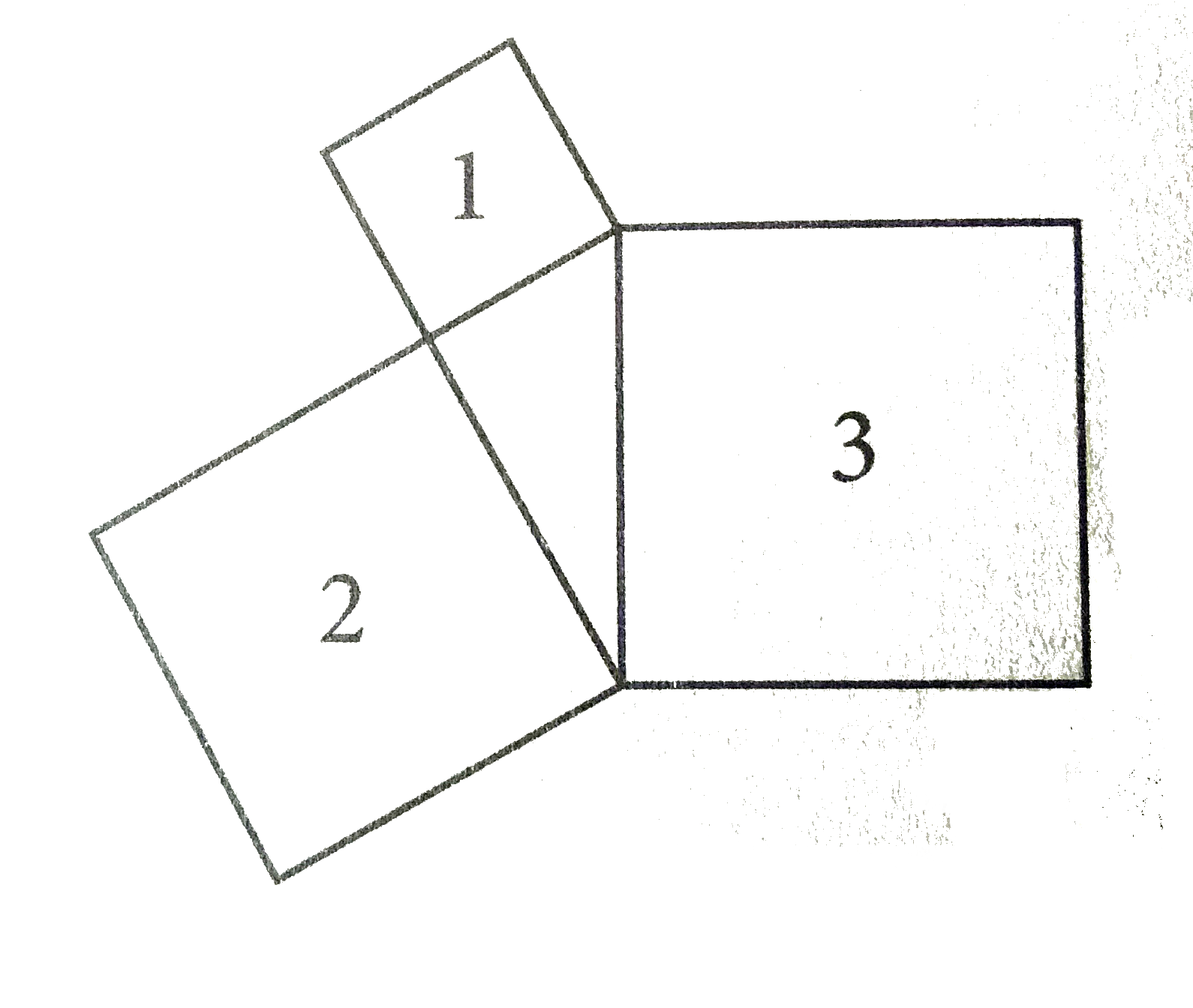
Each of the quadrilaterals figure above is a square. The area of the smallest square (square 1) is 16 square units, and the area of the medium square (square 2) is 48 square units. What is the area, in square units, of the largest square (square 3)?
View SolutionThe area of the largest possible square inscribed in a circle of unit radius ( in square unit ) is :
View SolutionIf the points ( k, k -1) , (k + 2 , k + 1) and (k , k +3) are three consective vertices of a square , then its area (in square units ) is _______.
View Solution
